【题目】如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
(1)求证:∠ADC=∠ABD;
(2)若AD=2 ![]() ,⊙O的半径为3,求MD的长.
,⊙O的半径为3,求MD的长.
参考答案:
【答案】
(1)证明:连接OD,如图:
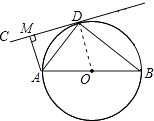
∵直线CD切⊙O于点D,∴∠CDO=90°,
∵AB为⊙O的直径,∴∠ADB=90°,
∴∠ADC+∠ADO=∠ADO+∠ODB=90°,∴∠ADC=∠ODB,
∵OB=OD,∴∠ODB=∠ADB,
∴∠ADC=∠ABD
(2)解:∵⊙O的半径为3,AB=6,
∵∠ADB=90°,∴DB═ ![]() ,
,
∵∠AMD=∠ADB=90°,∠ADC=∠ABD,
∴△ADM∽△ABD,
∴ ![]() ,即
,即 ![]()
∴DM=2 ![]()
【解析】(1)利用切线的性质定理,需连接OD,再利用直径所对圆周角是直角,可证出结论;(2)由(1)的结论结合垂直,可证出△ADM∽△ABD,对应边成比例可求出DM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠B=∠D.点EF分别在AB、CD上.连接AC,分别交DE、BF于G、H.求证:∠1+∠2=180°
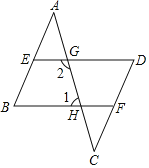
证明:∵AB∥CD,
∴∠B=_____._____
又∵∠B=∠D,
∴_____=_____.(等量代换)
∴_____∥_____._____
∴∠l+∠2=180°._____
-
科目: 来源: 题型:
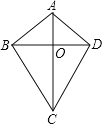
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S=
 ACBD.
ACBD.(1)写出正确结论的序号;
(2)证明所有正确的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校的北大门是由相同菱形框架组成的伸缩电动推拉门,如图是大门关闭时的示意图,此时 菱形的边长为0.5m,锐角都是50°.求大门的宽(结果精确到0.01,参考数据:sin25°≈0.422 6,cos25°≈0.906 3).
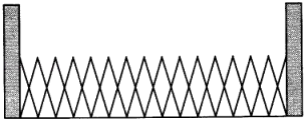
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x+b与反比例函数y=
 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b> 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y= 图象上的两点, 且y1>y2 , 求实数p的取值范围.
图象上的两点, 且y1>y2 , 求实数p的取值范围. -
科目: 来源: 题型:
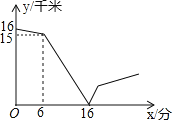
查看答案和解析>>【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示
(1)甲的速度为______千米/分,乙的速度为______千米/分
(2)当乙到达终点A后,甲还需______分钟到达终点B
(3)请通过计算回答:当甲、乙之间的距离为10千米时,甲出发了多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O的直径AB为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧
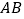 向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.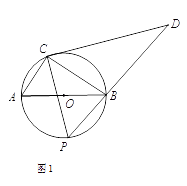
(1)求证:△ABC∽△PDC
(2)如图2,当点P到达B点时,求CD的长;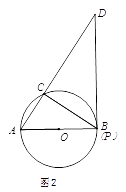
(3)设CD的长为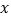 .在点P的运动过程中,
.在点P的运动过程中, 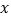 的取值范围为(请直接写出案).
的取值范围为(请直接写出案).
相关试题

