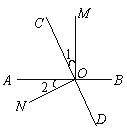
【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
参考答案:
【答案】(1)90°;(2)∠AOC=60°,∠MOD=150°.
【解析】(1)根据垂直的定义,可得∠AOC+∠1=90°由此易推出∠CON=90°,进而结合平角的定义即可解答本题;
(2)根据垂直可知∠AOM=∠BOM=90°,结合∠1=![]() ∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
解:(1)∵OM⊥AB,
∴∠AOM=90°,即∠AOC+∠1=90°.
∵∠1=∠2,∠AOC+∠1=90°,
∴∠AOC+∠2=90°,
即∠CON=90°,
∵∠CON+∠NOD=180°,
∴∠NOD=90°.
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°.
∵∠BOC=∠BOM+∠1,∠BOM=90°,∠1=![]() ∠BOC,
∠BOC,
∴∠1=30°.
∵∠AOC+∠1=∠AOM=90°,∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠MOD=∠MOB+∠AOC=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
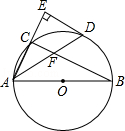
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
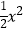 +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.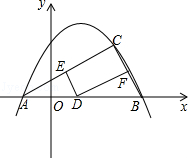
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
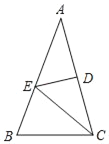
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个反比例函数y1=
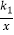 (其中k1>0)和y2=
(其中k1>0)和y2= 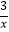 在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( ) 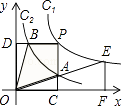
A.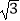 ﹕1
﹕1
B.2﹕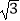
C.2﹕1
D.29﹕14 -
科目: 来源: 题型:
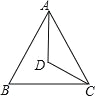
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,∠BAC 和∠ACB 的平分线相交于点D,∠ADC=125°,那么∠CAB 的大小是_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=
 ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 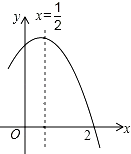
A.①②③④
B.③④
C.①③④
D.①②
相关试题

