【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 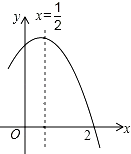
A.①②③④
B.③④
C.①③④
D.①②
参考答案:
【答案】A
【解析】解:∵二次函数的图象开口向下, ∴a<0,
∵二次函数的图象交y轴的正半轴于一点,
∴c>0,
∵对称轴是直线x= ![]() ,
,
∴﹣ ![]() =
= ![]() ,
,
∴b=﹣a>0,
∴abc<0.
故①正确;
∵由①中知b=﹣a,
∴a+b=0,
故②正确;
由对称轴为x= ![]() ,点(2,0)的对称点是(﹣1,0),
,点(2,0)的对称点是(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.
故③正确;
∵(0,y1)关于直线x= ![]() 的对称点的坐标是(1,y1),
的对称点的坐标是(1,y1),
∴y1=y2 .
故④正确;
综上所述,正确的结论是①②③④.
故选:A.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=
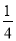 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD. 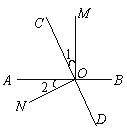
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个反比例函数y1=
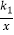 (其中k1>0)和y2=
(其中k1>0)和y2= 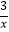 在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( ) 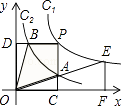
A.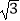 ﹕1
﹕1
B.2﹕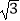
C.2﹕1
D.29﹕14 -
科目: 来源: 题型:
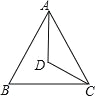
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,∠BAC 和∠ACB 的平分线相交于点D,∠ADC=125°,那么∠CAB 的大小是_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




相关试题

