【题目】△ABC中,AB=12,AC= ![]() ,∠B=30°,则△ABC的面积是 .
,∠B=30°,则△ABC的面积是 .
参考答案:
【答案】21 ![]() 或15
或15 ![]()
【解析】解:①如图1,作AD⊥BC,垂足为点D,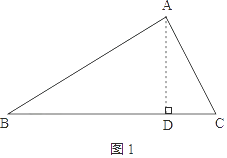
在Rt△ABD中,∵AB=12、∠B=30°,
∴AD= ![]() AB=6,BD=ABcosB=12×
AB=6,BD=ABcosB=12× ![]() =6
=6 ![]() ,
,
在Rt△ACD中,CD= ![]() =
= ![]() =
= ![]() ,
,
∴BC=BD+CD=6 ![]() +
+ ![]() =7
=7 ![]() ,
,
则S△ABC= ![]() ×BC×AD=
×BC×AD= ![]() ×7
×7 ![]() ×6=21
×6=21 ![]() ;
;
②如图2,作AD⊥BC,交BC延长线于点D,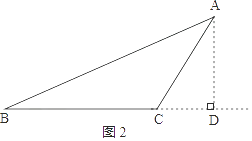
由①知,AD=6、BD=6 ![]() 、CD=
、CD= ![]() ,
,
则BC=BD﹣CD=5 ![]() ,
,
∴S△ABC= ![]() ×BC×AD=
×BC×AD= ![]() ×5
×5 ![]() ×6=15
×6=15 ![]() ,
,
故答案为:21 ![]() 或15
或15 ![]() .
.
由在直角三角形中,30度角所对的边是斜边的一半和余弦的定义,求出AD、BD=ABcosB的值,再由勾股定理求出BC=BD+CD的值,得到S△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).

(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
-
科目: 来源: 题型:
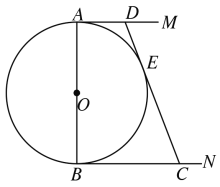
查看答案和解析>>【题目】如图,
 的直径
的直径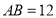 ,
,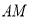 ,
,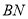 是
是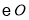 的两条切线,
的两条切线,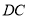 切
切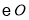 于
于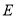 ,交
,交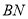 于
于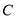 ,设
,设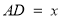 ,
,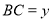 ,
, .
.
(1)求
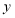 与
与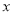 的函数关系式;
的函数关系式;(2)若
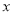 ,
,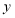 是
是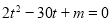 的两实根,求
的两实根,求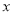 ,
,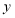 的值;
的值;(3)在(2)的前提下,求
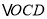 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=
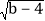 +
+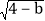 -6
-6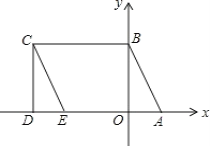
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+
 =0,过C作CB⊥x轴于B。
=0,过C作CB⊥x轴于B。
(1)求三角形ABC的面积;
(2)如图2,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.(
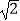 ≈1.4,
≈1.4, 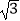 ≈1.7)
≈1.7)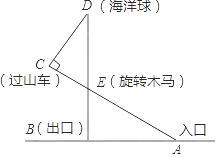
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
相关试题

