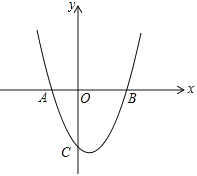
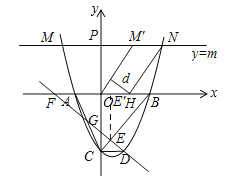
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为![]() .求点H到OM'的距离d的值.
.求点H到OM'的距离d的值.
参考答案:
【答案】(1)![]() ;(2)①n=﹣2;②△AGF与△CGD全等;(3)
;(2)①n=﹣2;②△AGF与△CGD全等;(3)![]() .
.
【解析】
试题分析:(1)根据抛物线![]() 与x轴交于A(﹣1,0),B(2,0)两点,可得抛物线的解析式;
与x轴交于A(﹣1,0),B(2,0)两点,可得抛物线的解析式;
(2)①过点E作EE'⊥x轴于E',则EE'∥OC,根据平行线分线段成比例定理,可得BE'=4OE',设点E的坐标为(x,y),则OE'=x,BE'=4x,根据OB=2,可得x的值,再根据直线BC的解析式即可得到E的坐标,把E的坐标代入直线y=﹣x+n,可得n的值;
②根据F(﹣2,0),A(﹣1,0),可得AF=1,再根据点D的坐标为(1,﹣3),点C的坐标为(0,﹣3),可得CD∥x轴,CD=1,再根据∠AFG=∠CDG,∠FAG=∠DCG,即可判定△AGF≌△CGD;
(3)根据轴对称的性质得出OH=1=M'N,进而判定四边形OM'NH是平行四边形,再根据四边形OM'NH的面积,求得OP的长,再根据点M的坐标得到PM'的长,Rt△OPM'中,运用勾股定理可得OM'的值,最后根据OM'×d=![]() ,即可得到d的值.
,即可得到d的值.
试题解析:(1)∵抛物线![]() 与x轴交于A(﹣1,0),B(2,0)两点,∴
与x轴交于A(﹣1,0),B(2,0)两点,∴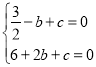 ,解得:
,解得: ,∴该抛物线的解析式
,∴该抛物线的解析式![]() ;
;
(2)①如图,过点E作EE'⊥x轴于E',则EE'∥OC,∴![]() ,∵BE=4EC,∴BE'=4OE',设点E的坐标为(x,y),则OE'=x,BE'=4x,∵B(2,0),∴OB=2,即x+4x=2,∴x=
,∵BE=4EC,∴BE'=4OE',设点E的坐标为(x,y),则OE'=x,BE'=4x,∵B(2,0),∴OB=2,即x+4x=2,∴x=![]() ,∵抛物线
,∵抛物线![]() 与y轴交于点C,∴C(0,﹣3),设直线BC的解析式为y=kx+b',∵B(2,0),C(0,﹣3),∴
与y轴交于点C,∴C(0,﹣3),设直线BC的解析式为y=kx+b',∵B(2,0),C(0,﹣3),∴![]() ,解得:
,解得: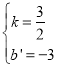 ,∴直线BC的解析式为
,∴直线BC的解析式为![]() ,当x=
,当x=![]() 时,y=﹣
时,y=﹣![]() ,∴E(
,∴E(![]() ,﹣
,﹣![]() ),把E的坐标代入直线y=﹣x+n,可得﹣
),把E的坐标代入直线y=﹣x+n,可得﹣![]() +n=﹣
+n=﹣![]() ,解得n=﹣2;
,解得n=﹣2;
②△AGF与△CGD全等.理由如下:
∵直线EF的解析式为y=﹣x﹣2,∴当y=0时,x=﹣2,∴F(﹣2,0),OF=2,∵A(﹣1,0),∴OA=1,∴AF=2﹣1=1,由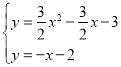 ,解得:
,解得: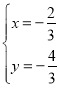 或
或![]() ,∵点D在第四象限,∴点D的坐标为(1,﹣3),∵点C的坐标为(0,﹣3),∴CD∥x轴,CD=1,∴∠AFG=∠CDG,∠FAG=∠DCG,∴△AGF≌△CGD;
,∵点D在第四象限,∴点D的坐标为(1,﹣3),∵点C的坐标为(0,﹣3),∴CD∥x轴,CD=1,∴∠AFG=∠CDG,∠FAG=∠DCG,∴△AGF≌△CGD;
(3)∵抛物线的对称轴为x=![]() =
=![]() ,直线y=m(m>0)与该抛物线的交点为M,N,∴点M、N关于直线x=
,直线y=m(m>0)与该抛物线的交点为M,N,∴点M、N关于直线x=![]() 对称,设N(t,m),则M(1﹣t,m),∵点 M关于y轴的对称点为点M',∴M'(t﹣1,m),∴点M'在直线y=m上,∴M'N∥x轴,∴M'N=t﹣(t﹣1)=1,∵H(1,0),∴OH=1=M'N,∴四边形OM'NH是平行四边形,设直线y=m与y轴交于点P,∵四边形OM'NH的面积为
对称,设N(t,m),则M(1﹣t,m),∵点 M关于y轴的对称点为点M',∴M'(t﹣1,m),∴点M'在直线y=m上,∴M'N∥x轴,∴M'N=t﹣(t﹣1)=1,∵H(1,0),∴OH=1=M'N,∴四边形OM'NH是平行四边形,设直线y=m与y轴交于点P,∵四边形OM'NH的面积为![]() ,∴OH×OP=1×m=
,∴OH×OP=1×m=![]() ,即m=
,即m=![]() ,∴OP=
,∴OP=![]() ,当
,当![]() =
=![]() 时,解得x1=﹣
时,解得x1=﹣![]() ,x2=
,x2=![]() ,∴点M的坐标为(﹣
,∴点M的坐标为(﹣![]() ,
,![]() ),∴M'(
),∴M'(![]() ,
,![]() ),即PM'=
),即PM'=![]() ,∴Rt△OPM'中,OM'=
,∴Rt△OPM'中,OM'=![]() =
=![]() ,∵四边形OM'NH的面积为
,∵四边形OM'NH的面积为![]() ,∴OM'×d=
,∴OM'×d=![]() ,∴d=
,∴d=![]() .
.
-
科目: 来源: 题型:
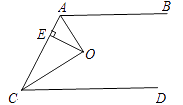
查看答案和解析>>【题目】如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,CO=3,则两平行线间AB、CD的距离等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判定直角三角形全等的方法,不正确的是( )
A. 斜边和一锐角对应相等
B. 两锐角对应相等
C. 两条直角边对应相等
D. 斜边和一条直角边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,∠1=∠2,∠B=∠C,则BD=CE.请说明理由:

解:∵∠1=∠2
∴∠1+∠BAC=∠2+ .
即=∠DAB.
在△ABD和△ACE中,
∠B=(已知)
∵AB= (已知)
∠EAC=(已证)
∴△ABD≌△ACE()
∴BD=CE( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
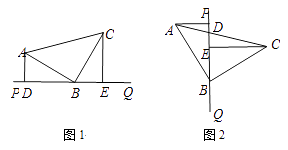
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD,DE,CE有怎样的等量关系?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A.a2a3=a5
B.(a2)3=a5
C.a6÷a2=a3
D.a5+a5=2a10
相关试题

