【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

参考答案:
【答案】(1)见解析(2) ∠AEB=15°(3) 见解析
【解析】试题分析:(1)由等边三角形的性质可得AB=AD,AE=AC,∠DAB=∠EAC=60°,即可得∠DAC=∠BAE,利用SAS即可判定△ABE≌△ADC;(2)根据全等三角形的性质即可求解;(3)由(1)的方法可证得△ABE≌△ADC,根据全等三角形的性质和等边三角形的性质可得∠AEB=∠ACD =60°,即可得∠AEB=∠EAC,从而得AC∥BE.
试题解析:
(1)证明:∵△ABD,△ACE都是等边三角形
∴AB=AD,AE=AC,
∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,
在△ABE和△ADC中,
∴ ,
,
∴△ABE≌△ADC;
(2)由(1)知△ABE≌△ADC,
∴∠AEB=∠ACD,
∵∠ACD=15°,
∴∠AEB=15°;
(3)同上可证:△ABE≌△ADC,
∴∠AEB=∠ACD,
又∵∠ACD=60°,
∴∠AEB=60°,
∵∠EAC=60°,
∴∠AEB=∠EAC,
∴AC∥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5
 千米的地方有一居民点B,A、B的直线距离是10
千米的地方有一居民点B,A、B的直线距离是10  千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
 的顶点都在方格纸的格点上,先将
的顶点都在方格纸的格点上,先将 向右平移2个单位,再向上平移3个单位,得到
向右平移2个单位,再向上平移3个单位,得到 ,其中点
,其中点 、
、 、
、 分别是A,B、C的对应点,试画出
分别是A,B、C的对应点,试画出 .
. 连接
连接 、
、 ,则线段
,则线段 、
、 的位置关系为______,线段
的位置关系为______,线段 、
、 的数量关系为______;
的数量关系为______; 平移过程中,线段AB扫过部分的面积为______
平移过程中,线段AB扫过部分的面积为______ 平方单位
平方单位

-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算: +(
+(  )﹣1﹣2cos60°+(2﹣π)0;
)﹣1﹣2cos60°+(2﹣π)0;
(2)化简: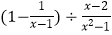 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
(1)y的值随x值的增大而 (填“增大”或“减小”);
(2)图象与x轴的交点坐标是 ;图象与y轴的交点坐标是 ;
(3)当x 时,y <0 ;
(4)直线y=-2x+3与两坐标轴所围成的三角形的面积是: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4
 ,CD=8.
,CD=8.(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

相关试题

