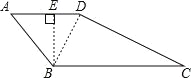
【题目】如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4![]() ,CD=8.
,CD=8.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

参考答案:
【答案】(1) 150°;(2) 4![]() +16.
+16.
【解析】试题分析:(1)连接BD,首先证明△ABD是等边三角形,可得∠ADB=60°,DB=4,再利用勾股定理逆定理证明△BDC是直角三角形,进而可得答案;
(2)过B作BE⊥AD,利用三角形函数计算出BE长,再利用△ABD的面积加上△BDC的面积可得四边形ABCD的面积.
试题解析:(1)连接BD,
∵AB=AD,∠A=60°,∴△ABD是等边三角形,∴∠ADB=60°,DB=4,
∵42+82=(4)2,∴DB2+CD2=BC2,∴∠BDC=90°,∴∠ADC=60°+90°=150°;
(2)过B作BE⊥AD,∵∠A=60°,AB=4,∴BE=ABsin60°=4×![]() =2
=2![]() ,
,
∴四边形ABCD的面积为:![]() ADEB+
ADEB+![]() DBCD=
DBCD=![]() ×4×2
×4×2![]() +
+![]() ×4×8=4
×4×8=4![]() +16.
+16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算: +(
+(  )﹣1﹣2cos60°+(2﹣π)0;
)﹣1﹣2cos60°+(2﹣π)0;
(2)化简: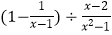 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
(1)y的值随x值的增大而 (填“增大”或“减小”);
(2)图象与x轴的交点坐标是 ;图象与y轴的交点坐标是 ;
(3)当x 时,y <0 ;
(4)直线y=-2x+3与两坐标轴所围成的三角形的面积是: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高天然气使用效率,保障居民的本机用气需求,某地积极推进阶梯式气价改革,若一户居民的年用气量不超过300m3,价格为2.5元/m3,若年用气量超过300m3,超出部分的价格为3元/m3,
(1)根据题意,填写下表:

(2)设一户居民的年用气量为xm3,付款金额为y元,求y关于x的解析式;
(3)若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)解分式方程: +
+  =
=  ;
;
(2)解不等式组 .
.
相关试题

