【题目】计算:
(1)(﹣5)+2![]() +(﹣
+(﹣![]() )+(﹣2
)+(﹣2![]() )
)
(2)![]()
(3) 365![]() (﹣13)+565÷13+1100÷13
(﹣13)+565÷13+1100÷13
(4)﹣22+3×(﹣1)4﹣(﹣4)×2.
参考答案:
【答案】(1)﹣5![]() ;(2)﹣22;(3)100;(4)7.
;(2)﹣22;(3)100;(4)7.
【解析】
(1)将原式去括号后相加减可得答案;
(2)利用乘法的分配律将括号内每个数除以﹣![]() 后相加减可得答案;
后相加减可得答案;
(3)将原式化为﹣365×![]() +565×
+565×![]() +1100×
+1100×![]() 用乘法的分配律计算即可;
用乘法的分配律计算即可;
(4)先算乘方后算乘法后相加减可得答案.
(1)(﹣5)+2![]() +(﹣
+(﹣![]() )+(﹣2
)+(﹣2![]() )
)
=﹣5+(2![]() ﹣2
﹣2![]() )+(﹣
)+(﹣![]() )
)
=﹣5+0﹣![]()
=﹣5![]() ;
;
(2)(![]() +
+![]() ﹣
﹣![]() )÷(﹣
)÷(﹣![]() )
)
=(![]() +
+![]() ﹣
﹣![]() )×(﹣42)
)×(﹣42)
=![]() ×(﹣42)+
×(﹣42)+![]() ×(﹣42)﹣
×(﹣42)﹣![]() ×(﹣42)
×(﹣42)
=﹣35﹣14+27
=﹣22;
(3)365÷(﹣13)+565÷13+1100÷13
=﹣365×![]() +565×
+565×![]() +1100×
+1100×![]()
=(﹣365+565+1100)×![]()
=1300×![]()
=100;
(4)﹣22+3×(﹣1)4﹣(﹣4)×2.
=﹣4+3+8
=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直接写出计算结果:
(1) -2-11 = (2) 5-(-12)=
(3) (-5)×(-6) = (4)

(5)
 = (6)
= (6)  =
=(7)-3.5+3.5 = (8)
 =
= -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
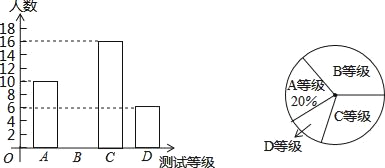
(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)请你计算扇形统计图中八年级学生体能测试结果为D等级的扇形圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD和△BCD都是等边三角形纸片,AB=2,将△ABD纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.
(1)求证:△FBE是直角三角形;
(2)求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.

(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=
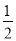 x﹣8的解.
x﹣8的解.①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
相关试题

