【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
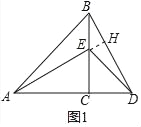
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

参考答案:
【答案】(1)AE=BD,AE⊥BD;(2)结论:AE=BD,AE⊥BD.理由见解析;(3)满足条件的AD的值为17或7.
【解析】
(1)如图1中,延长AE交BD于H.只要证明△ACE≌△BCD即可;
(2)结论不变.如图2中,延长AE交BD于H,交BC于O.只要证明△ACE≌△BCD即可;
(3)分两种情形分别求解即可解决问题;
(1)如图1中,延长AE交BD于H.
∵AC=CB,∠ACE=∠BCD,CE=CD,
∴△ACE≌△BCD,
∴AE=BD,∠EAC=∠CBD,
∵∠EAC+∠AEC=90°,∠AEC=∠BEH,
∴∠BEH+∠EBH=90°,
∴∠EHB=90°,即AE⊥BD,
(2)结论:AE=BD,AE⊥BD.
理由:如图2中,延长AE交BD于H,交BC于O.
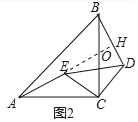
∵∠ACB=∠ECD=90°,
∴∠ACE=∠BCD,
∵AC=CB,∠ACE=∠BCD,CE=CD,
∴△ACE≌△BCD,
∴AE=BD,∠EAC=∠CBD,
∵∠EAC+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,即AE⊥BD.
(3)①当射线AD在直线AC的上方时,作CH⊥AD用H.
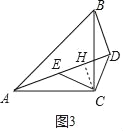
∵CE=CD,∠ECD=90°,CH⊥DE,
∴EH=DH,CH=![]() DE=5,
DE=5,
在Rt△ACH中,∵AC=13,CH=5,
∴![]()
∴AD=AH+DH=12+5=17.
②当射线AD在直线AC的下方时时,作CH⊥AD用H.
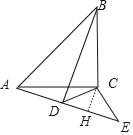
同法可得:AH=12,故AD=AH﹣DH=12﹣5=7,
综上所述,满足条件的AD的值为17或7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD和△BCD都是等边三角形纸片,AB=2,将△ABD纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.
(1)求证:△FBE是直角三角形;
(2)求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣5)+2
 +(﹣
+(﹣ )+(﹣2
)+(﹣2 )
)(2)
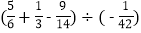
(3) 365
 (﹣13)+565÷13+1100÷13
(﹣13)+565÷13+1100÷13(4)﹣22+3×(﹣1)4﹣(﹣4)×2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.

(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=
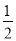 x﹣8的解.
x﹣8的解.①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式:__________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)琪琪用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

相关试题

