【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价一元,日销售量将减少20千克。
⑴现要保证每天盈利6000元,同时又要让顾客得到实惠,那么每千克应涨价多少元?
②若该商场单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多。
参考答案:
【答案】(1)涨价为![]() 元;(2)应涨价
元;(2)应涨价![]() 元,最大总利润为
元,最大总利润为![]() 元.
元.
【解析】
试题分析:(1)根据题意得,列出利润关系式,要保证每天盈利![]() 元,那么得到一元二次方向,即可求解;(2)利用配方法,可求出二次函数的最值;
元,那么得到一元二次方向,即可求解;(2)利用配方法,可求出二次函数的最值;
试题解析:(1)设每千克应涨价![]() 元,则
元,则![]()
解得![]() ,
,![]() ,
,
为了使顾客得到实惠,所以![]() .
.
(2)设涨价![]() 元时总利润为
元时总利润为![]() ,则
,则

当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
故应涨价![]() 元,最大总利润为
元,最大总利润为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:

由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为 km,流动加油车出发位置为 km;
(2)当两车同时开出x小时时,甲车位置为 km,流动加油车位置为 km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长为10, 7, 5, 3的四根木条,选其中三根首尾顺次相连接组成三角形,选法有( )
A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
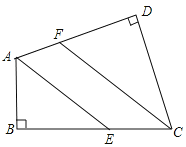
查看答案和解析>>【题目】已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2﹣4的图象与y轴的交点坐标是( )
A.(2,0)
B.(﹣2,0)
C.(0,4)
D.(0,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A.y=x2+3
B.y=x2﹣3
C.y=(x+3)2
D.y=(x﹣3)2
相关试题

