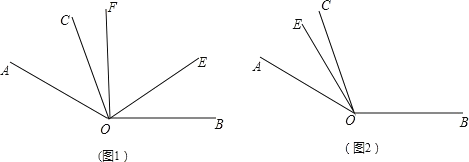
【题目】如图1,已知∠AOB=![]() ,∠AOC=
,∠AOC=![]() ,OE是∠AOB内部的一条射线,且OF平分∠AOE.
,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=![]() ,求∠COF的度数;
,求∠COF的度数;
(2)若∠COF=![]() ,求∠EOB的度数(用含n的式子表示);
,求∠EOB的度数(用含n的式子表示);
(3)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
参考答案:
【答案】(1)20°;(2)70°-2n°;(3)∠EOB=70°+2∠COF,理由见解析.
【解析】
(1)先求出∠AOE,再根据角平分线的定义求出∠AOF,然后根据∠COF=∠AOF-∠AOC代入数据计算即可得解;
(2)先求出∠AOF,再根据角平分线的定义求出∠AOE,然后根据∠EOB=∠AOB-∠AOE计算即可得解;
(3)设∠COF=n°,先表示出∠AOF,然后根据角平分线的定义求出∠AOE,再根据∠EOB=∠AOB-∠AOE代入计算即可得解.
解:(1)∵∠AOB=150°,∠EOB=30°,
∴∠AOE=∠AOB-∠EOB=150°-30°=120°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=
∠AOE=![]() ×120°=60°,
×120°=60°,
∴∠COF=∠AOF-∠AOC,
=60°-40°,
=20°;
(2)∵∠AOC=40°,∠COF=n°,
∴∠AOF=∠AOC+∠COF=40°+n°,
∵OF平分∠AOE,
∴∠AOE=2∠AOF=2(40°+n°)=80°+2n°,
∴∠EOB=∠AOB-∠AOE=150°-(80°+2n°)=70°-2n°;
(3)如图所示:∠EOB=70°+2∠COF.

证明:设∠COF=n°,则∠AOF=∠AOC-∠COF=40°-n°,
又∵OF平分∠AOE,
∴∠AOE=2∠AOF=80°-2n°.
∴∠EOB=∠AOB-∠AOE=150°-(80°-2n°)=(70+2n)°
即∠EOB=70°+2∠COF.
-
科目: 来源: 题型:
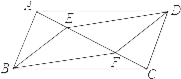
查看答案和解析>>【题目】如图,E、F是ABCD对角线AC上两点,且AE=CF.
(1)求证:四边形BFDE是平行四边形.
(2)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?
-
科目: 来源: 题型:
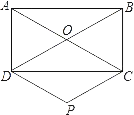
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C,D分别作BD,AC的平行线,两线相交于点P.
(1)求证:四边形CODP是菱形;
(2)当矩形ABCD的边AD,DC满足什么关系时,菱形CODP是正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.
(1)用含x的代数式表示:每件商品的销售价为 元,每件商品的利润为 元,每周的商品销售量为 件;
(2)求y关于x的函数关系式(不要求写出x的取值范围);
(3)应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数:
0,3,8,15,24,…①
2,5,10,17,26,…②
0,6,16,30,48,…③
(1)第①行数按什么规律排的,请写出来?
(2)第②、③行数与第①行数分别对比有什么关系?
(3)取每行的第
 个数,求这三个数的和.
个数,求这三个数的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,一个数在数轴上所对应的点与原点之间的距离就是这个数的绝对值。那么任意两个数与它们在数轴上所对应的点之间的距离又有什么关系呢?
(1)如图所示,-3,-1,2,4在数轴上分别对应点
 。
。
则①点
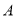 与原点之间的距离为_______________;②
与原点之间的距离为_______________;②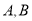 两点之间的距离为_____________;
两点之间的距离为_____________;③
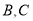 两点之间的距离为______________;④
两点之间的距离为______________;④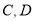 两点之间的距离为_______________。
两点之间的距离为_______________。你的结论:如果两个数
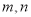 在数轴上分别对应点
在数轴上分别对应点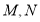 ,那么
,那么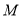 与
与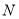 两点之间的距离表示为______________________。(用含
两点之间的距离表示为______________________。(用含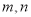 的式子表示)
的式子表示)(2)利用(1)的结论解决下列问题:
已知数轴上点
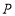 对应
对应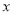 ,点
,点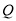 对应3,且
对应3,且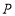 与
与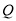 之间的距离是8,求
之间的距离是8,求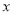 的值。
的值。
相关试题

