搜索
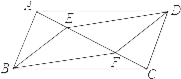
【题目】如图，E、F是ABCD对角线AC上两点，且AE＝CF．
（1）求证：四边形BFDE是平行四边形．
（2）如果把条件AE＝CF改为BE＝DF，试问四边形BFDE还是平行四边形吗？为什么？
参考答案：
【答案】（1）详见解析；（2）四边形BFDE不是平行四边形，理由详见解析.
【解析】
（1）根据对角线互相平分的四边形是平行四边形即可证明；
（2）四边形BFDE不是平行四边形.
（1）证明：连接BD，交AC于点O．
∵ABCD是平行四边形
∴OA＝OC OB＝OD（平行四边形的对角线互相平分）
又∵AE＝CF
∴OA﹣AE＝OC﹣CF，即OE＝OF
∴四边形BFDE是平行四边形（对角线互相平分的四边形是平行四边形）
（2）四边形BFDE不是平行四边形
因为把条件AE＝CF改为BE＝DF后，不能证明△BAE与△DCF全等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，线段AB=24，动点P从A出发，以每秒2个单位的速度沿射线AB运动，运动时间为t秒(t>0)，点M为AP的中点.
（1）当点P在线段AB上运动时.当t为多少时，AM=6.
（2）当点P在AB延长线上运动时，点N为BP的中点，求出线段MN的长度.
（3）在P点的运动过程中，点N为BP的中点，是否存在这样的t的值，使M、N、B三点中的一个点是以其余两点为端点的线段的中点，若有，请求出t的值；若没有，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知△ABC中，AB＝BC＝1，∠ABC＝90°，把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转．
（1）在图1中，DE交AB于M，DF交BC于N．
①求证:DM＝DN；
②在这一旋转过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的？若不发生变化，求出其面积；
（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM＝DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM＝DN是否仍然成立？请写出结论，不用证明．
-
科目： 来源： 题型：
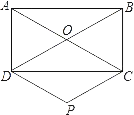
查看答案和解析>>【题目】已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，过点C，D分别作BD，AC的平行线，两线相交于点P．
（1）求证：四边形CODP是菱形；
（2）当矩形ABCD的边AD，DC满足什么关系时，菱形CODP是正方形？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商品的进货价为每件30元，为了合理定价，先投放市场试销．据市场调查，销售价为每件40元时，每周的销售量是180件，而销售价每上涨1元，则每周的销售量就会减少5件，设每件商品的销售价上涨x元，每周的销售利润为y元．
（1）用含x的代数式表示：每件商品的销售价为 元，每件商品的利润为 元，每周的商品销售量为 件；
（2）求y关于x的函数关系式（不要求写出x的取值范围）；
（3）应怎样确定销售价，使该商品的每周销售利润最大？最大利润是多少？
-
科目： 来源： 题型：
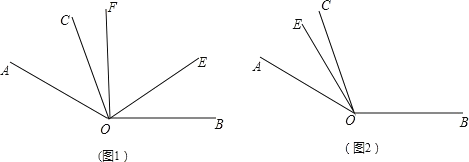
查看答案和解析>>【题目】如图1,已知∠AOB=
,∠AOC=
，OE是∠AOB内部的一条射线，且OF平分∠AOE.(1)若∠EOB=
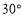，求∠COF的度数；(2)若∠COF=
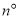，求∠EOB的度数(用含n的式子表示）；(3)当射线OE绕点O逆时针旋转到如图2的位置时，请把图补充完整；此时，∠COF与∠EOB有怎样的数量关系?请说明理由.
相关试题
