【题目】如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C、D的坐标及四边形ABDC的面积;
(2)若点Q在线的CD上移动(不包括C,D两点).QO与线段AB,CD所成的角∠1与∠2如图所示,给出下列两个结论:①∠1+∠2的值不变;②![]() 的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
(3)在y轴正半轴上是否存在点P,使得S△CDP=S△PBO?如果有,试求出点P的坐标.

参考答案:
【答案】(1)C(0,2)、D(5,2);S四边形ABDC=10;(2)∠1+∠2=180°;证明见解析;(3)存在,点P的坐标为(0,![]() )或(0,5).
)或(0,5).
【解析】
(1)依据平移与坐标变化的规律可求的点C、D的坐标,由点的坐标可求得AB、OC的长,从而可求得四边形ABDC的面积;
(2)依据平行的性质可证明∠1+∠2=180°;
(3)设点P的坐标(0,a),然后依据三角形的面积公式列方程求解即可.
(1)OA=2,OB=3,
∴A(﹣2,0)、B(3,0).
∵将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,
∴C(0,2)、D(5,2).
∵由平移的性质可知:AB∥CD,AB=CD,
∴ABCD为平行四边形.
∴四边形ABDC的面积=ABOC=5×2=10.
(2)∠1+∠2=180°.
证明:如图1所示;
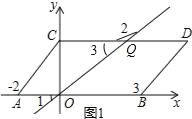
∵AB∥CD,
∴∠1=∠3.
∵∠3+∠2=180°.
∴∠1+∠2=180°.
∴∠1+∠2为定值.
∵∠1+∠2=180°,
∴∠2=180°﹣∠1.
∴![]() =
=![]() =
=![]() ﹣1.
﹣1.
∵当点Q在CD上运动时,∠1的度数在不断变化,
∴![]() ﹣1在不断变化,即
﹣1在不断变化,即![]() 的值在不断变化;
的值在不断变化;
(3)如图2所示:设点P的坐标为(0,a),则PC=(2﹣a),PO=a.
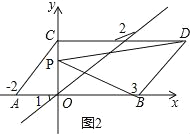
∵S△CDP=S△PBO,
∴![]() DCPC=
DCPC=![]() OBOP.
OBOP.
∴![]() ×5(2﹣a)=
×5(2﹣a)=![]() ×3×a.
×3×a.
∴10﹣5a=3a
解得:a=![]()
如图3所示:设点P的坐标为(0,a),则PC=a﹣2,PO=a.
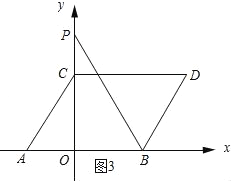
∵SCDP=S△PBO,
∴![]() DCPC=
DCPC=![]() OBOP.
OBOP.
∴![]() ×5×(a﹣2)=
×5×(a﹣2)=![]() ×3×a.
×3×a.
∴5a﹣10=3a.
解得:a=5.
综上所述,点P的坐标为(0,![]() )或(0,5).
)或(0,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求一次函数y=2x-2的图象l1与y=
 x-1的图象l2的交点P的坐标.
x-1的图象l2的交点P的坐标.(2)求直线
 与
与 轴交点A的坐标; 求直线
轴交点A的坐标; 求直线 与x轴的交点B的坐标;
与x轴的交点B的坐标;(3)求由三点P、A、B围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
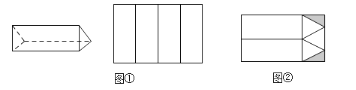
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
-
科目: 来源: 题型:
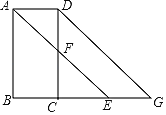
查看答案和解析>>【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+4ax+4a-4(a≠0)的顶点为A.
(1)求顶点A的坐标;
(2)过点(0,5)且平行于x轴的直线l,与抛物线y=ax2+4ax+4a-4(a≠0)交于B、C两点.
①当a=1时,求线段BC的长;
②当线段BC的长不小于8时,直接写出a的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点. 定义图形W的测度面积:若|x1-x2|的最大值为m,|y1-y2|的最大值为n,则S=mn为图形W的测度面积. 例如,若图形W是半径为l的⊙O. 当P,Q分别是⊙O与x轴的交点时,如图1,|x1-x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1-y2|取得最大值,且最大值n=2. 则图形W的测度而积S=mn=4.

(1)若图形W是抛物线y=-x2+2x+3和直线y=2x-1围成的封闭图形,则它的测度面积S=______

(2)若图形W是一个边长为1的正方形ABCD.
①当A,B两点均在x轴上时,它的测度面积S=_________;
②此图形测度面积S的最大值为_________;
(3)若图形W是一个边长分别为3和6的矩形ABCD,求它的测度面积S的取值范围.
相关试题

