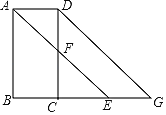
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
参考答案:
【答案】(1)∠DCG=87°;(2)AD∥BC,理由见解析;(3)当α=2β时,AE∥DG.理由见解析.
【解析】
(1)根据平行线的判定定理得到AB∥CD,由平行线的性质得到∠DCG=∠B=87°;
(2)由平行线的性质得到∠BAF=∠CFE,根据角平分线的定义得到∠BAF=∠FAD,等量代换得到∠DAF=∠CFE,∠DAF=∠AEB,由平行线的判定即可得到结论;
(3)根据平行线的判定定理得到∠DAF=∠AEB,根据角平分线的定义得到∠DAB=2∠DAF=2∠AEB,然后根据平行线的性质即可得到结论.
(1)∵∠BAD+∠ADC=180°,
∴AB∥CD,
∴∠DCG=∠B=87°;
(2)AD∥BC,理由如下:
∵AB∥CD,
∴∠BAF=∠CFE,
又∵AE平分∠BAD,
∴∠BAF=∠FAD,
∴∠DAF=∠CFE,
而∠CFE=∠AEB,
∴∠DAF=∠AEB,
∴AD∥BC;
(3)当α=2β时,AE∥DG.理由:
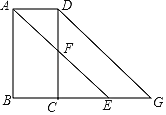
若AE∥DG,则∠G=∠AEB=∠DAE=![]() ∠BAD,
∠BAD,
即当∠BAD=2∠G时,AE∥DG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求一次函数y=2x-2的图象l1与y=
 x-1的图象l2的交点P的坐标.
x-1的图象l2的交点P的坐标.(2)求直线
 与
与 轴交点A的坐标; 求直线
轴交点A的坐标; 求直线 与x轴的交点B的坐标;
与x轴的交点B的坐标;(3)求由三点P、A、B围成的三角形的面积.
-
科目: 来源: 题型:
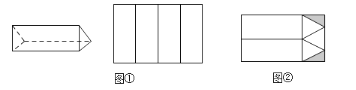
查看答案和解析>>【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C、D的坐标及四边形ABDC的面积;
(2)若点Q在线的CD上移动(不包括C,D两点).QO与线段AB,CD所成的角∠1与∠2如图所示,给出下列两个结论:①∠1+∠2的值不变;②
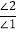 的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.(3)在y轴正半轴上是否存在点P,使得S△CDP=S△PBO?如果有,试求出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+4ax+4a-4(a≠0)的顶点为A.
(1)求顶点A的坐标;
(2)过点(0,5)且平行于x轴的直线l,与抛物线y=ax2+4ax+4a-4(a≠0)交于B、C两点.
①当a=1时,求线段BC的长;
②当线段BC的长不小于8时,直接写出a的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
相关试题

