【题目】如图,在平面直角坐标系中,直线y=﹣ ![]() x﹣
x﹣ ![]() 与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣
与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣ ![]() x+c(a≠0)经过A,B,C三点.
x+c(a≠0)经过A,B,C三点.
(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;
(2)在抛物线上是否存在点P,使△ABP为直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由;
(3)试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵直线y=﹣ ![]() x﹣
x﹣ ![]() 与x轴交于点A,与y轴交于点C
与x轴交于点A,与y轴交于点C
∴点A(﹣1,0),C(0,﹣ ![]() )
)
∵点A,C都在抛物线上,
∴ 
∴ 
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]()
![]() x﹣
x﹣ ![]()
∴顶点F(1,﹣ ![]() )
)
(2)
解:方法一:存在:
p1(0,﹣ ![]() ),p2(2,﹣
),p2(2,﹣ ![]() )
)
方法二:
设P(t, ![]() ),A(﹣1,0),B(3,0),
),A(﹣1,0),B(3,0),
∵PA⊥PB,∴KPA×KPB=﹣1,
![]() =﹣1,
=﹣1,
∴(t+1)(t﹣3)=﹣3,∴t1=0,t2=2,
∴P1(0,﹣ ![]() ),P2(2,﹣
),P2(2,﹣ ![]() ).
).
(3)
解:存在
理由:
解法一:
延长BC到点B′,使B′C=BC,连接B′F交直线AC于点M,则点M就是所求的点,
∵过点B′作B′H⊥AB于点H,
∵B点在抛物线y= ![]() x2﹣
x2﹣ ![]()
![]() x﹣
x﹣ ![]() 上,
上,
∴B(3,0),
在Rt△BOC中,tan∠OBC= ![]()
∴∠OBC=30°,BC=2 ![]()
在Rt△B′BH中,B′H= ![]() BB′=2
BB′=2 ![]()
BH= ![]() B′H=6,∴OH=3,
B′H=6,∴OH=3,
∴B′(﹣3,﹣2 ![]() ).
).
设直线B′F的解析式为y=kx+b,
∴  ,
,
解得  ,
,
∴y= ![]() .
.
 ,
,
解得  ,
,
∴M( ![]() )
)
∴在直线AC上存在点M,使得△MBF的周长最小,此时M( ![]() ).
).
解法二:
过点F作AC的垂线交y轴于点H,则点H为点F关于直线AC的对称点,连接BH交AC于点M,则点M
即为所求.
过点F作FG⊥y轴于点G,则OB∥FG,BC∥FH,
∴∠BOC=∠FGH=90°,∠BCO=∠FHG
∴∠HFG=∠CBO
同方法一可求得B(3,0)
在Rt△BOC中,tan∠OBC= ![]()
∴∠OBC=30°,可求得GH=GC= ![]()
∴GF为线段CH的垂直平分线,可证得△CFH为等边三角形
∴AC垂直平分FH
即点H为点F关于AC对称点,
∴H(0,﹣ ![]() )
)
设直线BH的解析式为y=kx+b,由题意得,  ,
,
解得  ,
,
∴y= ![]() ,
,
 ,
,
解得  ,
,
∴M( ![]() ),
),
∴在直线AC上存在点M,使得△MBF的周长最小,此时M( ![]() )
)



【解析】(1)抛物线解析式中有两个待定系数a,c,根据直线AC解析式求点A、C坐标,代入抛物线解析式即可;(2)分析不难发现,△ABP的直角顶点只可能是P,根据已知条件可证AC2+BC2=AB2 , 故点C满足题意,根据抛物线的对称性,点C关于抛物线对称轴的对称点也符合题意;(3)由于B,F是定点,BF的长一定,实际上就是求BM+FM最小,找出点B关于直线AC的对称点B',连接B'F,交AC于点M,点M即为所求,由(2)可知,BC⊥AC,延长BC到B',使BC=B'C,利用中位线的性质可得B'的坐标,从而可求直线B'F的解析式,再与直线AC的解析式联立,可求M点坐标.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中: ①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 . (请写出所有正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小方格都是边长为1个单位长度的小正方形.

(1)将△ABC向右平移3个单位长度,画出平移后的△A1B1C1 .
(2)将△ABC绕点O旋转180°,画出旋转后的△A2B2C2 .
(3)画出一条直线将△AC1A2的面积分成相等的两部分. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.

(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)如图3,如果α=45°,AB=2,AE=4 ,求点G到BE的距离.
,求点G到BE的距离. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
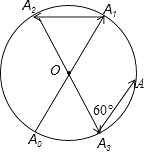
A.4
B.2
C.2
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边三角形OAB与反比例函数y=
 (k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则
(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则  的值为 . (已知sin15°=
的值为 . (已知sin15°=  )
)
相关试题

