【题目】如图,已知等边三角形OAB与反比例函数y= ![]() (k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则
(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则 ![]() 的值为 . (已知sin15°=
的值为 . (已知sin15°= ![]() )
)
参考答案:
【答案】![]()
【解析】解:如图,过O作OM⊥x轴于M,
∵△AOB是等边三角形,
∴AM=BM,∠AOM=∠BOM=30°,
∴A、B关于直线OM对称,
∵A、B两点在反比例函数y= ![]() (k>0,x>0)的图象上,且反比例函数关于直线y=x对称,
(k>0,x>0)的图象上,且反比例函数关于直线y=x对称,
∴直线OM的解析式为:y=x,
∴∠BOD=45°﹣30°=15°,
过B作BF⊥x轴于F,过C作CN⊥x轴于N,
sin∠BOD=sin15°= ![]() =
= ![]() ,
,
∵∠BOC=60°,∠BOD=15°,
∴∠CON=45°,
∴△CNO是等腰直角三角形,
∴CN=ON,
设CN=x,则OC= ![]() x,
x,
∴OB= ![]() x,
x,
∴ ![]() =
= ![]() ,
,
∴BF= ![]() ,
,
∵BF⊥x轴,CN⊥x轴,
∴BF∥CN,
∴△BDF∽△CDN,
∴ ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣
 x﹣
x﹣  与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣
与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣  x+c(a≠0)经过A,B,C三点.
x+c(a≠0)经过A,B,C三点.
(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;
(2)在抛物线上是否存在点P,使△ABP为直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由;
(3)试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.

(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)如图3,如果α=45°,AB=2,AE=4 ,求点G到BE的距离.
,求点G到BE的距离. 
-
科目: 来源: 题型:
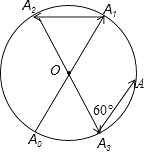
查看答案和解析>>【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
A.4
B.2
C.2
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表分数段
频数
频率
60≤x<70
18
0.36
70≤x<80
17
c
80≤x<90
a
0.24
90≤x≤100
b
0.06
合计
1
根据以上信息解答下列问题:

(1)统计表中c的值为;样本成绩的中位数落在分数段中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
相关试题

