【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了![]() 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
第 | 第 | 第 | 第 | 第 | |
甲成绩 |
|
|
|
|
|
乙成绩 |
|
|
|
|
|
(1)a=_________
(2)![]()
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.

参考答案:
【答案】(1)4;(2)6;(3)1.6;(4)乙将被选中,详见解析
【解析】
(1)根据两人的总成绩相同,进而求出a的值;
(2)根据平均数的计算方法即可;
(3)直接利用方差公式求出即可;
(4)利用平均数以及方差的意义分析得出即可.
解:(1)∵两人各射了5箭,他们的总成绩相同,
甲的总成绩为:9+4+7+4+6=30;
∴乙的总成绩为:7+5+7+a+7=30,解得:a=4,
(2)由(1)可知:![]()
![]() ×30=6,
×30=6,
(3)![]() =
=![]() [(76)2+(56)2+(76)2+(46)2+(76)2]=1.6;
[(76)2+(56)2+(76)2+(46)2+(76)2]=1.6;
(4)因为两人成绩的平均水平(平均数)相同,由于![]() ,
,
所以乙的成绩比甲稳定,所以乙将被选中.
-
科目: 来源: 题型:
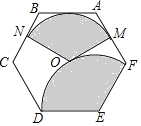
查看答案和解析>>【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

-
科目: 来源: 题型:
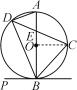
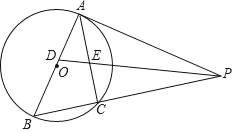
查看答案和解析>>【题目】如图:C、D是以AB为直径的⊙O上的点,
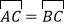 ,弦CD交AB于点E.
,弦CD交AB于点E.(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2-CE2=CE·DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 为
为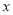 轴负半轴上一点,
轴负半轴上一点,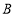 为
为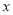 轴正半轴上一点,
轴正半轴上一点,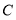 点坐标为
点坐标为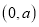 ,
,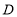 点坐标
点坐标 为且
为且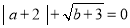 .
.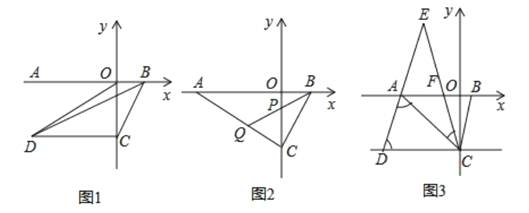
(1)求
 两点的坐标;
两点的坐标;(2)求
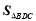 ;
;(3)如图2,若
 点坐标为
点坐标为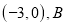 点坐标为
点坐标为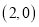 ,点
,点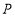 为线段
为线段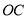 上一点,
上一点,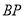 的延长线交线段
的延长线交线段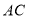 于点
于点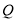 ,若
,若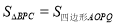 ,求出点
,求出点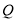 坐标.
坐标.(4)如图3,若
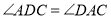 ,点
,点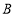 在
在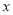 轴正半轴上任意运动,
轴正半轴上任意运动,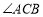 的平分线
的平分线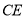 交
交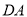 的延长线于点
的延长线于点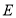 ,在
,在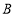 点的运动过程中,
点的运动过程中,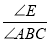 的值是否发生变化,若不变化,求出比值;若变化请说明理由.
的值是否发生变化,若不变化,求出比值;若变化请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=
 ,DE=
,DE= ,求AD的长.
,求AD的长.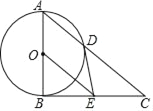
相关试题

