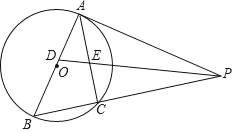
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
参考答案:
【答案】(1)证明见解析;(2)存在,![]()
【解析】(1)易证∠APE=∠BPD,∠EAP=∠B,从而可知△PAE∽△PBD,利用相似三角形的性质即可求出答案.
(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,易求得AE=2,BD=3,由(1)可知:![]() ,从而可知cos∠BDF=cos∠BAC=cos∠APC=
,从而可知cos∠BDF=cos∠BAC=cos∠APC=![]() ,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
(1)∵PD平分∠APB,
∴∠APE=∠BPD,
∵AP与⊙O相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB是⊙O的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴![]() ,
,
∴PABD=PBAE;
(2)如图,过点D作DF⊥PB于点F,作DG⊥AC于点G,
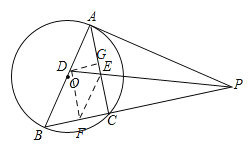
∵PD平分∠APB,AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x2﹣5x+6=0的两个实数根,
解得:AE=2,BD=3,
∴由(1)可知:![]() ,
,
∴cos∠APC=![]() ,
,
∴cos∠BDF=cos∠APC=![]() ,
,
∴![]() ,
,
∴DF=2,
∴DF=AE,
∴四边形ADFE是平行四边形,
∵AD=DF,
∴四边形ADFE是菱形,此时点F即为M点,
∵cos∠BAC=cos∠APC=![]() ,
,
∴sin∠BAC=![]() ,
,
∴![]() ,
,
∴DG=![]() ,
,
∴菱形ADME的面积为:DGAE=2×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:C、D是以AB为直径的⊙O上的点,
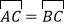 ,弦CD交AB于点E.
,弦CD交AB于点E.(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2-CE2=CE·DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了
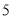 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).第
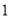 次
次第
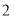 次
次第
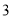 次
次第
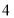 次
次第
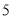 次
次甲成绩
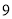
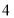
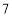
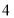
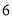
乙成绩
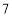
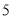
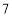

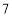
(1)a=_________
(2)
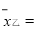
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.

-
科目: 来源: 题型:
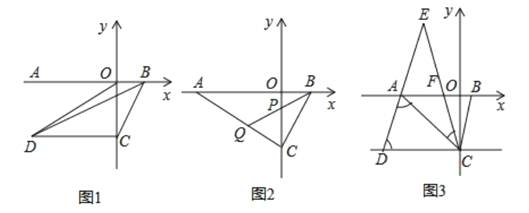
查看答案和解析>>【题目】如图1,
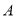 为
为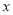 轴负半轴上一点,
轴负半轴上一点,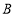 为
为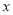 轴正半轴上一点,
轴正半轴上一点,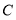 点坐标为
点坐标为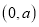 ,
,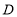 点坐标
点坐标 为且
为且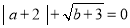 .
.
(1)求
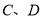 两点的坐标;
两点的坐标;(2)求
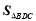 ;
;(3)如图2,若
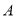 点坐标为
点坐标为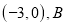 点坐标为
点坐标为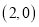 ,点
,点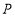 为线段
为线段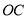 上一点,
上一点,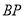 的延长线交线段
的延长线交线段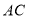 于点
于点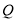 ,若
,若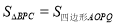 ,求出点
,求出点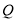 坐标.
坐标.(4)如图3,若
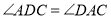 ,点
,点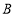 在
在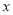 轴正半轴上任意运动,
轴正半轴上任意运动,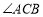 的平分线
的平分线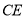 交
交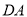 的延长线于点
的延长线于点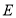 ,在
,在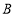 点的运动过程中,
点的运动过程中,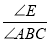 的值是否发生变化,若不变化,求出比值;若变化请说明理由.
的值是否发生变化,若不变化,求出比值;若变化请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=
 ,DE=
,DE= ,求AD的长.
,求AD的长.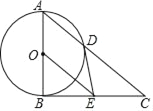
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数
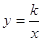 的图象上.那么k的值是
的图象上.那么k的值是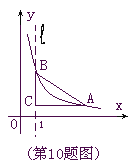
A .3 B.6 C.12 D.
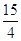
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
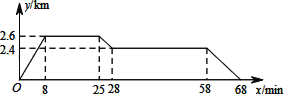
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
相关试题

