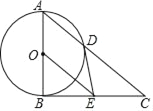
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】(1)DE是⊙O的切线,理由见解析;(2)证明见解析;(3)![]()
【解析】(1)先判断出DE=BE=CE,得出∠DBE=∠BDE,进而判断出∠ODE=90°,即可得出结论;
(2)先判断出△BCD∽△ACB,得出BC2=CDAC,再判断出DE=![]() BC,AC=2OE,即可得出结论;
BC,AC=2OE,即可得出结论;
(3)先求出BC,进而求出BD,CD,再借助(2)的结论求出AC,即可得出结论.
(1)DE是⊙O的切线,理由:如图,
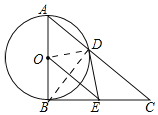
连接OD,BD,∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°,
∵OE∥AC,OA=OB,
∴BE=CE,
∴DE=BE=CE,
∴∠DBE=∠BDE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODE=∠OBE=90°,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠BCD=∠ABC=90°,∠C=∠C,
∴△BCD∽△ACB,
∴![]() ,
,
∴BC2=CDAC,
由(1)知DE=BE=CE=![]() BC,
BC,
∴4DE2=CDAC,
由(1)知,OE是△ABC是中位线,
∴AC=2OE,
∴4DE2=CD2OE,
∴2DE2=CDOE;
(3)∵DE=![]() ,
,
∴BC=5,
在Rt△BCD中,tanC=![]() ,
,
设CD=3x,BD=4x,根据勾股定理得,(3x)2+(4x)2=25,
∴x=-1(舍)或x=1,
∴BD=4,CD=3,
由(2)知,BC2=CDAC,
∴AC=![]() ,
,
∴AD=AC-CD=![]() -3=
-3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了
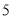 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).第
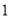 次
次第
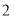 次
次第
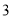 次
次第
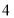 次
次第
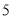 次
次甲成绩
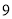
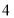
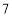
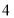
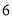
乙成绩
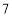
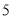
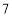

(1)a=_________
(2)
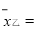
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.

-
科目: 来源: 题型:
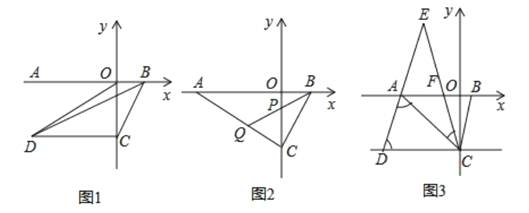
查看答案和解析>>【题目】如图1,
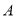 为
为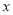 轴负半轴上一点,
轴负半轴上一点,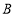 为
为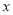 轴正半轴上一点,
轴正半轴上一点,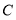 点坐标为
点坐标为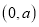 ,
, 点坐标
点坐标 为且
为且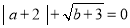 .
.
(1)求
 两点的坐标;
两点的坐标;(2)求
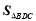 ;
;(3)如图2,若
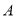 点坐标为
点坐标为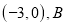 点坐标为
点坐标为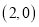 ,点
,点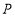 为线段
为线段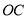 上一点,
上一点,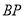 的延长线交线段
的延长线交线段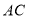 于点
于点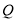 ,若
,若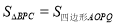 ,求出点
,求出点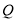 坐标.
坐标.(4)如图3,若
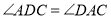 ,点
,点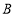 在
在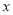 轴正半轴上任意运动,
轴正半轴上任意运动,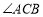 的平分线
的平分线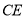 交
交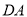 的延长线于点
的延长线于点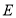 ,在
,在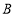 点的运动过程中,
点的运动过程中,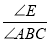 的值是否发生变化,若不变化,求出比值;若变化请说明理由.
的值是否发生变化,若不变化,求出比值;若变化请说明理由. -
科目: 来源: 题型:
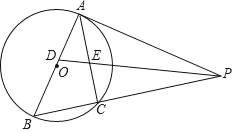
查看答案和解析>>【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数
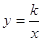 的图象上.那么k的值是
的图象上.那么k的值是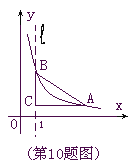
A .3 B.6 C.12 D.
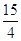
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
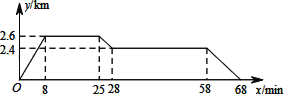
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACE是以平行四边行ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(10,-4
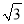 ),则D点的坐标是( )
),则D点的坐标是( )
A.(6,0)B.(6
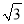 ,0)C.(8,0)D.(8
,0)C.(8,0)D.(8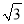 ,0)
,0)
相关试题

