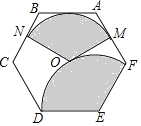
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
参考答案:
【答案】![]()
【解析】根据题意正六边形中心角为120°且其内角为120°.求出两个扇形圆心角,表示出扇形半径即可.
连OA
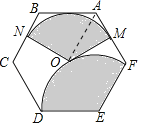
由已知,M为AF中点,则OM⊥AF
∵六边形ABCDEF为正六边形
∴∠AOM=30°
设AM=a
∴AB=AO=2a,OM=![]()
∵正六边形中心角为60°
∴∠MON=120°
∴扇形MON的弧长为:![]()
则r1=![]() a
a
同理:扇形DEF的弧长为:![]()
则r2=![]()
r1:r2=![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,每个小方格的边长为一个单位长度.
(1)点
 的坐标为 .点
的坐标为 .点 的坐标为 .
的坐标为 .(2)点
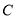 关于
关于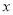 轴对称点的坐标为 ;
轴对称点的坐标为 ;(3)以
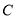 、
、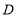 、
、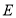 为顶点的三角形的面积为 ;
为顶点的三角形的面积为 ;(4)点
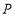 在
在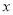 轴上,且
轴上,且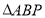 的面积等于
的面积等于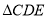 的面积,点
的面积,点 的坐标为 .
的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
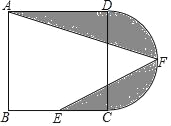
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系xOy中,A(4,0)、B(0,3)、C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )
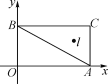
A. (-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:C、D是以AB为直径的⊙O上的点,
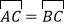 ,弦CD交AB于点E.
,弦CD交AB于点E.(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2-CE2=CE·DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了
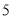 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).第
 次
次第
 次
次第
 次
次第
 次
次第
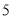 次
次甲成绩
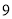
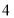
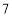
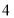
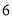
乙成绩
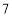
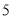
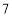

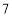
(1)a=_________
(2)
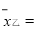
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.

相关试题

