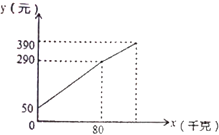
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数![]() 与他手中持有的钱数
与他手中持有的钱数![]() 元(含备用零钱)的关系如图所示,结合图象回答下列问题:
元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是390元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
参考答案:
【答案】(1)50元;(2)3元;(3)他一共批发了120千克的西瓜;(4)一共赚了124元钱.
【解析】
(1)售卖西瓜0时手中的钱为自带的钱;
(2)售卖80千克前是按照市场价出售,用对应钱数-自带的钱后,除售卖重量可得;
(3)先算出降价后售卖的西瓜,然后加上降价前的80千克西瓜可得;
(4)最终的钱减去自带的钱,然后在减掉成本可得
解:(1)由图可得农民自带的零钱为50元,
(2)降价前他每千克西瓜出售的价格是3元;
![]() 元,
元,
(3)他一共批发了120千克的西瓜;
![]() (千克),
(千克),
![]() 千克,
千克,
(4)这个水果贩子一共赚了124元钱
![]() 元,
元,
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式变形中,正确的是( )
A.2x23x3=6x6
B.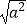 =a
=a
C.x2﹣4=(x+4)(x﹣4)
D.(a﹣b)2=(b﹣a)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
-
科目: 来源: 题型:
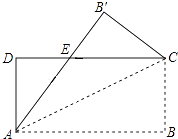
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,现将一直角三角形
,现将一直角三角形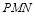 放入图中,其中
放入图中,其中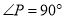 ,
,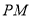 交
交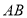 于点
于点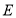 ,
,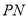 交
交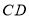 于点
于点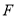
(1)当
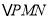 所放位置如图①所示时,则
所放位置如图①所示时,则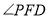 与
与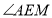 的数量关系为_______;请说明理由.
的数量关系为_______;请说明理由.(2)当
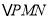 所放位置如图②所示时,
所放位置如图②所示时,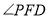 与
与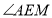 的数量关系为________;
的数量关系为________;(3)在(2)的条件下,若
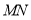 与
与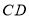 交于点0,且
交于点0,且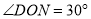 ,
,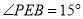 ,求
,求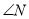 的度数.
的度数.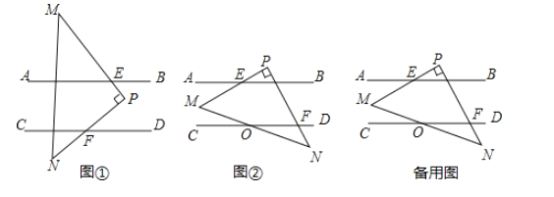
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个长为
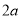 、宽为
、宽为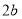 的长方形(
的长方形(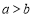 ),沿图1中虚线用剪刀分成四块相同的小长方形,并将
),沿图1中虚线用剪刀分成四块相同的小长方形,并将 块小长方形彼此不重叠拼成一个正方形(如图2)
块小长方形彼此不重叠拼成一个正方形(如图2)(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含
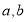 的代数式表示).
的代数式表示).(2)利用图2存在的面积关系,直接写出下列三个代数式
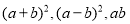 之间的等量关系: .
之间的等量关系: .(3)如图3,已知长方形的周长为
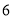 ,面积为
,面积为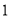 ,试求该长方形长与宽的差.
,试求该长方形长与宽的差.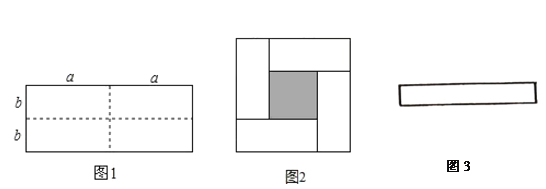
相关试题

