搜索
【题目】下列各式变形中，正确的是（ ）
A.2x23x3=6x6
B.
=a
C.x2﹣4=（x+4）（x﹣4）
D.（a﹣b）2=（b﹣a）2
参考答案：
【答案】D
【解析】解：A、原式=6x5，故A错误；
B、原式|a|，故B错误；
C、原式（x+2）（x﹣2），故C错误；
所以答案是：D
【考点精析】本题主要考查了二次根式的性质与化简和单项式乘单项式的相关知识点，需要掌握1、如果被开方数是分数（包括小数）或分式，先利用商的算数平方根的性质把它写成分式的形式，然后利用分母有理化进行化简．2、如果被开方数是整数或整式，先将他们分解因数或因式，然后把能开得尽方的因数或因式开出来；单项式与单项式相乘，把他们的系数，相同字母的幂分别相乘，其余字母连同他的指数不变，作为积的因式才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】不能够铺满地面的组合图形是（ ）
A. 正八边形和正方形 B. 正方形和正三角形
C. 正六边形和正方形 D. 正六边形和正三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线AB、CD相交于点O，OE平分∠BOD．OF⊥CD，垂足为O，若∠EOF＝54°．
（1）求∠AOC的度数；
（2）作射线OG⊥OE，试求出∠AOG的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线y=
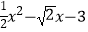与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为点D，过点B作BC的垂线，交对称轴于点E．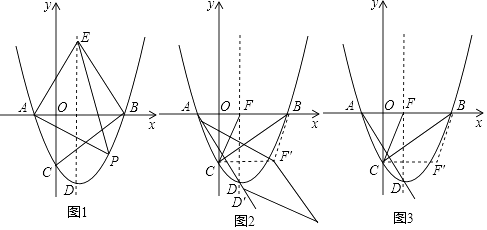
（1）求证：点E与点D关于x轴对称；
（2）点P为第四象限内的抛物线上的一动点，当△PAE的面积最大时，在对称轴上找一点M，在y轴上找一点N，使得OM+MN+NP最小，求此时点M的坐标及OM+MN+NP的最小值；
（3）如图2，平移抛物线，使抛物线的顶点D在射线AD上移动，点D平移后的对应点为D′，点A的对应点A′，设抛物线的对称轴与x轴交于点F，将△FBC沿BC翻折，使点F落在点F′处，在平面内找一点G，若以F′、G、D′、A′为顶点的四边形为菱形，求平移的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O为直线AB上一点，过点O作射线OC，使∠BOC=135°，将一个含45°角的直角三角尺的一个顶点放在点O处，斜边OM与直线AB重合，另外两条直角边都在直线AB的下方．
（1）将图1中的三角尺绕着点O逆时针旋转90°，如图2所示，此时∠BOM=_____；在图2中，OM是否平分∠CON？请说明理由；
（2）紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示，使得ON在∠AOC的内部，请探究：∠AOM与∠CON之间的数量关系，并说明理由；
（3）将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为_____（直接写出结果）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落在点B′的位置，AB′与CD交于点E，若AB=8，AD=3，则△EB′C的周长为 ．
-
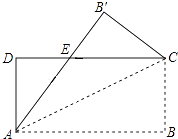
科目： 来源： 题型：
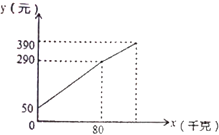
查看答案和解析>>【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售，为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数
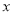与他手中持有的钱数
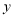元（含备用零钱）的关系如图所示，结合图象回答下列问题：（1）农民自带的钱是多少？
（2）降价前他每千克西瓜出售的价格是多少？
（3）随后他按每千克下降0.5元将剩余的西瓜售完，这时他手中的钱（含备用的钱）是390元，问他一共批发了多少千克的西瓜？
（4）请问这个水果贩子一共赚了多少钱？
相关试题
