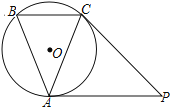
【题目】已知:AB=AC,PA=PC,若PA为△ABC的外接圆⊙O的切线
(1) 求证:PC为⊙O的切线;
(2) 连接BP,若sin∠BAC=![]() ,求tan∠BPC的值.
,求tan∠BPC的值.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1) 连接OA、OC, 证明△OAP≌△OCP,即可求出![]() 即可证明.
即可证明.
![]() 连接AO,并延长交BC于D,连接OB、OC,得到BC∥PA,根据sin∠BAC=sin∠BOD=
连接AO,并延长交BC于D,连接OB、OC,得到BC∥PA,根据sin∠BAC=sin∠BOD=![]() ,设BD=3,OB=5,则OD=4, 根据sin∠APC=sin∠PCE=
,设BD=3,OB=5,则OD=4, 根据sin∠APC=sin∠PCE=![]() ,
,
求出PC=15,CE=12, 过点C作CF⊥BP于F ,证明△BCF∽△BPE,求出![]() 的长即可求解.
的长即可求解.
详解:(1) 连接OA、OC,
∵PA为⊙O的切线,
∴∠OCP=90°,
连接OP,
可证:△OAP≌△OCP(SSS),
∴∠OAP=∠OCP=90°,
∴PC为⊙O的切线,
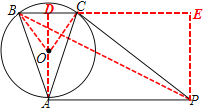
(2) 连接AO,并延长交BC于D,连接OB、OC,
∵AB=AC,OB=OC∴AD为线段BC的垂直平分线,
∴AD⊥BC∵AD⊥AP,
∴BC∥PA,
∵sin∠BAC=sin∠BOD=![]() ∴设BD=3,OB=5,则OD=4,
∴设BD=3,OB=5,则OD=4,
∵∠PAC=∠ACB,且AB=AC,PA=PC,
∴∠BAC=∠APC过点P作PE⊥BC交BC的延长线于E,
∴四边形APED为矩形 ,
∴PE=AD=9 ,
∴sin∠APC=sin∠PCE=![]() ,PC=15,CE=12,
,PC=15,CE=12,
过点C作CF⊥BP于F ,
∵△BCF∽△BPE
∴![]() ,CF=
,CF=![]() ,BF=
,BF=![]() ,PF=
,PF=![]() ∴tan∠BPC=
∴tan∠BPC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果品基地购买某种优质水果慰问医务工作者,果品基地对购买量在3000kg以上(含3000kg)的顾客采用两种销售方案.甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费用为5000元.
(1)分别写出该公司两种购买方案付款金额y(元)与所购买的水果量x(kg)之间的函数关系式.
(2)当购买量在哪一范围时,选择哪种购买方案付款最少?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)33.1﹣10.7﹣(﹣229)﹣|﹣
 |
|(2)

(3)(﹣36)×

(4)4﹣(﹣2)

(5)﹣3﹣[﹣5+(1﹣2×
 )÷(﹣2)]
)÷(﹣2)](6)(﹣96)×(﹣0.125)+96×
 +(﹣96)×
+(﹣96)×
(7)﹣14+(﹣3)×[(﹣4)2+2]﹣(﹣2)3÷4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AM是中线,D是AM所在直线上的一个动点(不与点A重合),DE∥AB交AC所在直线于点F,CE∥AM,连接BD,AE.

(1)如图1,当点D与点M重合时,观察发现:△ABM向右平移
 BC到了△EDC的位置,此时四边形ABDE是平行四边形.请你给予验证;
BC到了△EDC的位置,此时四边形ABDE是平行四边形.请你给予验证;(2)如图2,图3,图4,是当点D不与点M重合时的三种情况,你认为△ABM应该平移到什么位置?直接在图中画出来.此时四边形ABDE还是平行四边形吗?请你选择其中一种情况说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的“图书角”平均每天借出图书 50 册.如果某天借出 51 册,就记作+1;如果某天借出 45 册,就记作-5.上星期该“图书角”借出图书数量记录如下表:
星期一
星期二
星期三
星期四
星期五
0
+10
+4
-3
-6
(1)上星期五借出图书多少册?
(2)上星期二比上星期五多借出图书多少册?
(3)上星期平均每天借出图书多少册?
-
科目: 来源: 题型:
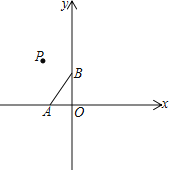
查看答案和解析>>【题目】已知:平面直角坐标系中,点A(-2,0)、B(0,3),点P为第二象限内一点
(1) 如图,将线段AB绕点P旋转180°得线段CD,点A与点C对应,试画出图形;
(2) 若(1)中得到的点C、D恰好在同一个反比例函数
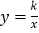 的图象上,试求直线BC的解析式;
的图象上,试求直线BC的解析式;(3) 若点Q(m,n)为第四象限的一点,将线段AB绕点Q顺时针旋转90°到点E、F.若点E、F恰好在同一个反比例函数的图象上,试直接写出m、n之间的关系式__________________.
相关试题

