【题目】点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0
![]()
(1)求线段AB的长;
(2)如图1 点C在数轴上对应的数为x,且x是方程2x+1=![]() x-5的根,在数轴上是否存在点P使PA+PB=
x-5的根,在数轴上是否存在点P使PA+PB=![]() BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
(3)如图2,若P点是B点右侧一点,PA的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,有两个结论:①PM-![]() BN的值不变;②
BN的值不变;②![]() PM+
PM+![]() BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
参考答案:
【答案】(1)5;(2)点P对应的数是-4.5或3.5;(3)正确的结论是:PM-![]() BN的值不变,且值为2.5.
BN的值不变,且值为2.5.
【解析】
试题分析:(1)利用非负数的性质求出a与b的值,即可确定出AB的长;(2)求出已知方程的解确定出x,得到C表示的点,设点P在数轴上对应的数是m,由PA+PB=![]() BC+AB确定出P位置,即可做出判断;(3)设P点所表示的数为n,就有PN=n+3,PB=n-2,根据条件就可以表示出PM=
BC+AB确定出P位置,即可做出判断;(3)设P点所表示的数为n,就有PN=n+3,PB=n-2,根据条件就可以表示出PM=![]() ,BN=
,BN=![]() ×(n-2),再分别代入①PM-
×(n-2),再分别代入①PM-![]() BN和②
BN和②![]() PM+
PM+![]() BN求出其值即可.
BN求出其值即可.
试题解析:(1)∵|a+3|+(b-2)2=0,
∴a+3=0,b-2=0,
∴a=-3,b=2,
∴AB=|-3-2|=5.
答:AB的长为5;
(2)∵2x+1=![]() x-5,
x-5,
∴x=-4,
∴BC=6.
设点P在数轴上对应的数是m,
∴PA+PB=![]() BC+AB=
BC+AB=![]() ×6+5=8,
×6+5=8,
当P在B点右侧时
5+2BP=8,
BP= ![]() ,
,
∴点P对应的数为![]() +2=
+2=![]() 。
。
当P在B点左侧时
5+2AP=8,
AP= ![]() ,
,
∴点P对应的数为-3-![]() =
=![]() 。
。
∴点P对应的数是-4.5或3.5;
(3)设P点所表示的数为n,
∴PN=n+3,PB=n-2.
∵PA的中点为M,
∴PM=![]() PN=
PN=![]()
N为PB的三等分点且靠近于P点,
∴BN=![]() PB=
PB=![]() ×(n-2).
×(n-2).
∴PM-![]() BN=
BN=![]() -
-![]() ×
×![]() ×(n-2)=
×(n-2)=![]() (不变).
(不变).
②![]() PM+
PM+![]() BN=
BN=![]() +
+![]() ×
×![]() ×(n-2)=
×(n-2)=![]() n-
n-![]() (随P点的变化而变化).
(随P点的变化而变化).
∴正确的结论是:PM-![]() BN的值不变,且值为2.5.
BN的值不变,且值为2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】右图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即ABCDCBABC…的方式)从A开始数连续的正整数1,2,3,4…,当数到12时,对应的字母是 ;当字母C第201次出现时,恰好数到的数是 ;当字母C第2n+1次出现时(n为正整数),恰好数到的数是 (用含n的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB是∠AOC的余角,∠AOD是∠AOC的补角,且∠BOD=2∠BOC,求∠BOD、∠AOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
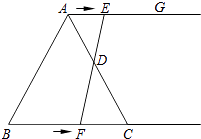
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,
 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=
 (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

相关试题

