【题目】(数学实验)如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干个可以拼出一些长方形来解释某些等式.例如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.

(初步运用)
(1)仿照例子,图③可以解释为: ;
(2)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+3b)、(a+5b),不画图形,试通过计算说明需要C类卡片多少张;
(拓展运用)
若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积为2a2+5ab+3b2,通过操作你会发现拼成的长方形的长宽分别是 ,将2a2+5ab+3b2改写成几个整式积的形式为 .
参考答案:
【答案】(1)a2+2ab+b2;(2)15张;(3)2a+3b,a+b,(2a+3b)(a+b).
【解析】
(1)根据图②结合图形的面积即可得到结论;
(2)根据多项式乘多项式的法则即可得到结论;
(3)根据已知条件可画出图形,于是得到矩形的两边.
(1)图③可以解释为:(a+b)(a+b)=a2+2ab+b2;
故答案为:a2+2ab+b2;
(2)∵(2a+3b)(a+5b)=2a2+13ab+15b2,
∴需要C类卡片15张;
(3)如图:
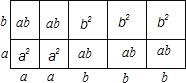
长方形的长是2a+3b,宽是a+b,2a2+5ab+3b2=(2a+3b)(a+b).
故答案为:2a+3b,a+b,(2a+3b)(a+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一条直线过点(0,4),且与抛物线y=
 x2交于A,B两点,其中点A的横坐标是﹣2.
x2交于A,B两点,其中点A的横坐标是﹣2.
(1)求这条直线的函数关系式及点B的坐标.
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.

(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=5,AB=7,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战初三物理、化学实验操作考试.某校对初三学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.小张同学对物理的①、②和化学的b、c实验准备得较好,请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b和反比例函数y2=
 的图象交于A、B两点.
的图象交于A、B两点.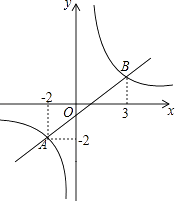
(1)求一次函数y1=kx+b和反比例函数y2= 的解析式;
的解析式;
(2)观察图象写出y1<y2时,x的取值范围为;
(3)求△OAB的面积. -
科目: 来源: 题型:
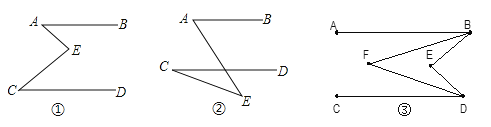
查看答案和解析>>【题目】(1)如图①、②,AB∥CD,你能说明∠A、∠E、∠C的关系吗?(请在图形下的横线上写出其关系并选一个进行说明)
(2)如图③若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80,则∠BFD=________.
相关试题

