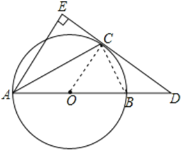
【题目】如图,点C是以AB为直径的⊙O上一点,CD是⊙O切线,D在AB的延长线上,作AE⊥CD于E.
(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求⊙O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?请证明你的结论.

参考答案:
【答案】(1)详见解析;(2)⊙O的半径是2![]() ;(3)CD2=BDAD,证明详见解析
;(3)CD2=BDAD,证明详见解析
【解析】
(1)连接OC,由CD是⊙O切线得到OC⊥CD,根据平行线的性质得到∠EAC=∠ACO,由等腰三角形的性质得到∠CAO=∠ACO,于是得到结论;
(2)连接BC,由三角函数的定义得到sin∠CAE=![]() ,得到∠CAE=30°,于是可得∠CAB=∠CAE=30°,由AB是⊙O的直径,得到∠ACB=90°,解直角三角形即可求解;
,得到∠CAE=30°,于是可得∠CAB=∠CAE=30°,由AB是⊙O的直径,得到∠ACB=90°,解直角三角形即可求解;
(3)根据余角的性质得到∠DCB=∠ACO,再得到△BCD∽△CAD,根据相似三角形的性质即可求解.
(1)证明:连接OC,
∵CD是⊙O切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠EAC=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠EAC=∠A=CAO,
即AC平分∠BAE;
(2)解:连接BC,
∵AE⊥CE,AC=2CE=6,
∴sin∠CAE=![]() ,
,
∴∠CAE=30°,
∴∠CAB=∠CAE=30°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴cos∠CAB=![]()
,
∴AB=4![]() ,
,
∴⊙O的半径是2![]() ;
;
(3)CD2=BDAD,
证明:∵∠DCB+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠DCB=∠ACO,
∴∠DCB=∠ACO=∠CAD,
∵∠D=∠D,
∴△BCD∽△CAD,
∴![]() ,
,
即CD2=BDAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=
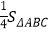 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.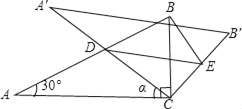
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x-
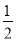 x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=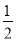 x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )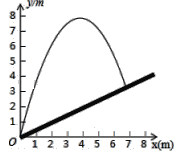
A.斜坡的坡度为1: 2
B.小球距O点水平距离超过4米呈下降趋势
C.小球落地点距O点水平距离为7米
D.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知将抛物线
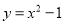 沿
沿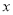 轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点
轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点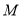 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点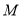 叫做“整点”).现将抛物线
叫做“整点”).现将抛物线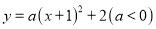 沿
沿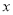 轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则
轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则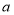 的取值范围是( )
的取值范围是( )
A.
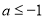 B.
B.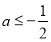 C.
C.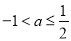 D.
D.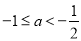
相关试题

