【题目】已知数轴上有A、B、C三个点,分别表示有理数-12、-5、5,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为 t秒。

(1)用含t的代数式表示P到点A和点C的距离:PA=________ , PC=________。
(2)当点P从点A出发,向点C移动,点Q以每秒3个单位从点C出发,向终点A移动,请求出经过几秒点P与点Q两点相遇?
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A,在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由。
参考答案:
【答案】(1))t;27-t;(2)经过4.25秒点P与点Q两点相遇;(3)点P表示的数为-![]() , -
, -![]() ,
, ![]() ,
, ![]() .
.
【解析】
(1)根据P点位置进而得出PA,PC的距离;
(2)根据两点运动路程之和等于线段AC的长即可得到方程求解;
(3)分别根据P点与Q点相遇前以及相遇后进而分别分析得出即可.
(1)t;27-t
(2)依题可得:
PA=t,CQ=3t,
∵P、Q两点相遇,
∴t+3t=5-(-12),
解得:t= ![]() =4.25,
=4.25,
答:经过4.25秒点P与点Q两点相遇.
(3)依题可得:
AP=t,AC=5+12=17,
∵动点P的速度是每秒1个单位,
∴点P运动到B点时间为:(-5+12)÷1=7(秒),
①当点P在点Q右侧,且Q点还没有追上P点时(如图1),
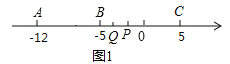
∵动点Q的速度是每秒3个单位,
∴AQ=3(t-7),
∵P、Q两点之间的距离为2个单位,
∴AP=AQ+PQ,
即3(t-7)+2=t,
解得:t=;
∴OP=OA-AP=12-![]() =
=![]() ,
,
∴点P表示的数为:-![]() ;
;
②当点P在点Q左侧,且Q点追上了P点时(如图2),
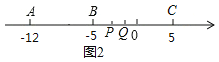
∵动点Q的速度是每秒3个单位,
∴AQ=3(t-7),
∵P、Q两点之间的距离为2个单位,
∴AQ=AP+PQ,
即3(t-7)=2+t,
解得:t=![]() ;
;
∴OP=OA-AP=12-![]() =
=![]() ,
,
∴点P表示的数为:-![]() .
.
③当点Q到达C点后,且P点在Q点左侧时(如图3),
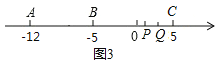
∵动点Q的速度是每秒3个单位,
∴AC+CQ=3(t-7),
∵AC=17,
∴CQ=3(t-7)-17,
∵P、Q两点之间的距离为2个单位,
∴AP+PQ+CQ=AC,
即t+2+3(t-7)-17=17,
解得:t=![]() ;
;
∴OP=AP-OA=![]() -12=
-12=![]() ,
,
∴点P表示的数为:![]() ;
;
④当点Q到达C点后,且P点在Q点右侧时(如图4),
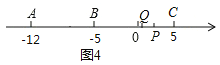
∵AP=t,PQ=2,
∴AQ=AP-PQ=t-2,
∵动点Q的速度是每秒3个单位,
∴AC+CQ=3(t-7),
∵AC=17,
∴CQ=3(t-7)-17,
∵P、Q两点之间的距离为2个单位,
∴AQ+CQ=AC,
即t-2+3(t-7)-17=17,
解得:t=![]() ;
;
∴OP=AP-OA=![]() -12=
-12=![]() ,
,
∴点P表示的数为:![]() .
.
综上所述:点P表示的数为-![]() ,-
,-![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,然后按要求解答问题:
例题:已知二次三项式
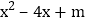 有一个因式是
有一个因式是 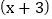 ,求另一个因式以及
,求另一个因式以及 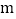 的值.
的值.解法一:设另一个因式为
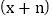 ,
,得
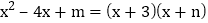 ,
,则
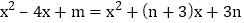 ,
,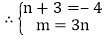 ,
,解得
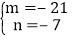 ,
, 另一个因式为
另一个因式为 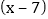 ,
,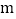 的值为
的值为 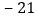 .
.解法二:∵二次三项式 x2-4x+m 有一个因式是 (x+3),
∴当x+3=0,即x=-3时,x2-4x+m=0.
把x=-3代入x2-4x+m=0,
得m=-21,
而x2-4x-21=(x+3)(x-7).
问题:分别仿照以上两种方法解答下面问题:
(1)已知二次三项式
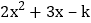 有一个因式是
有一个因式是 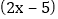 ,求另一个因式以及
,求另一个因式以及 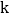 的值.
的值.解法一: 解法二:
(2)直接回答:
已知关于x的多项式 2x3
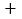 (3
(3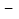 k)x2
k)x2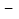 2x
2x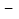 1有一个因式是
1有一个因式是 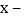 1,则k的值为_________.
1,则k的值为_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】先计算,再找出规律,然后根据规律进行计算.
(1)计算:①
 ②
② ③
③
(2)根据(1)中的计算,用字母表示出你发现的规律.
 =__________________
=__________________(3)根据(2)中的结论,计算下列结果:
①

②

③

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣2x的图象与二次函数y=﹣x2+3x图象的对称轴交于点B.

(1)写出点B的坐标;
(2)已知点P是二次函数y=﹣x2+3x图象在y轴右侧部分上的一个动点,将直线y=﹣2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:跳绳,B:跑操,C:舞蹈,D:健美操共四项活动,为了了解学生最喜欢哪一种活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有 人.
(2)请将条形统计图补充完整.
(3)求出扇形统计图中A项目对应的圆心角的度数.
-
科目: 来源: 题型:
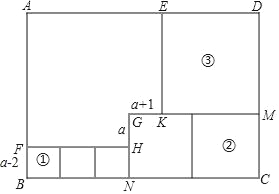
查看答案和解析>>【题目】如图所示,用三种大小不等的正方形①②③和…个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=a,GK=a+1,BF=a﹣2
(1)试用含a的代数式表示:正方形②的边长CM的长= ,正方形③的边长DM的长= ;
(2)求长方形ABCD的周长(用含a的代数式表示);并求出当a=3时,长方形周长的值.
-
科目: 来源: 题型:
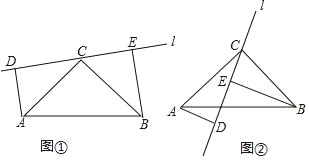
查看答案和解析>>【题目】探究:如图①,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的同侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.求证:DE=AD+BE.
应用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的异侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.直接写出线段AD、BE、DE之间的相等关系.
相关试题

