【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行统计,并绘制出了如图1和图2所示的统计图,根据图中信息解答下列问题:

(1)这天共销售了多少个粽子?
(2)销售B品牌粽子多少个?并补全图1中的条形图;
(3)求出A品牌粽子在图2中所对应的圆心角的度数;
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.
参考答案:
【答案】(1) 2400 个;(2) 800 个;(3) 60°;(4)见解析.
【解析】
(1)用C品牌的销售量除以它所占的百分比即可得销售这三种品牌粽子总个数;
(2)B品牌的销售量=总销售量1200400=800个,补全图形即可;
(3)A品牌粽子在图中所对应的圆心角的度数=360°×(400÷2400)=60°;
(4)由于C品牌的销售量最大,所以建议多进C种.
(1)销售粽子总数为![]() =2400(个);
=2400(个);
(2)销售B品牌粽子个数为2400﹣1200﹣400=800(个),
补全图1中的条形图,如下:

(3)A品牌粽子在图7中所对应的圆心角的度数为![]() ×360°=60°;
×360°=60°;
(4)根据上述统计信息,明年端午节期间该商场应多进C品牌的粽子,或者少进A品牌的粽子等.
-
科目: 来源: 题型:
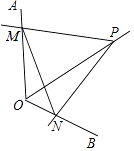
查看答案和解析>>【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数 (
( 为常数,且
为常数,且 )的图像交于
)的图像交于 两点.
两点.(1)求反比例函数的表达式;
(2)在
 轴上找一点
轴上找一点 ,使
,使 的值最小,求满足条件的点
的值最小,求满足条件的点 的坐标;
的坐标;(3)在(2)的条件下求
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AE=4,则△EBF周长的大小为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求,解答下列问题:
(1)解答下列问题 ①方程x2﹣2x+1=0的解为;
②方程x2﹣3x+2=0的解为;
③方程x2﹣4x+3=0的解为;
…
(2)根据以上方程特征及其解的特征,请猜想: ①方程x2﹣9x+8=0的解为;
②关于x的方程的解为x1=1,x2=n.
(3)请用配方法解方程x2﹣9x+8=0,以验证猜想结论的正确性. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲
63
66
63
61
64
61
乙
63
65
60
63
64
63
(Ⅰ)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(Ⅱ)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对情况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形. (Ⅰ)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形. (Ⅰ)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
(Ⅱ)若菱形ABEF的周长为16,AE=4 ,求∠C的大小.
,求∠C的大小.
相关试题

