Question

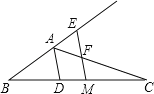
【题目】如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F．

（1）求证：AE=AF；

（2）求证：BE=（AB+AC）．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

试题分析：（1）根据角平分线的性质及平行线的性质易∠AEF=∠AFE，即可得AE=AF；（2）作CG∥EM，交BA的延长线于G，已知AC=AG，根据三角形中位线定理的推论证明BE=EG，再利用三角形的中位线定理即可证得结论．

试题解析：

（1）∵DA平分∠BAC，

∴∠BAD=∠CAD，

∵AD∥EM，

∴∠BAD=∠AEF，∠CAD=∠AFE，

∴∠AEF=∠AFE，

∴AE=AF．

（2）作CG∥EM，交BA的延长线于G．

∵EF∥CG，

∴∠G=∠AEF，∠ACG=∠AFE，

∵∠AEF=∠AFE，

∴∠G=∠ACG，

∴AG=AC，

∵BM=CM．EM∥CG，

∴BE=EG，

∴BE=BG=（BA+AG）=（AB+AC）．