【题目】综合题。
(1)解方程:x2=2x.
(2)如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC向右平移至△A′B′C′的位置,使得四边形ABB′A′为菱形,求B′C的长. 
参考答案:
【答案】
(1)解:∵x2﹣2x=0,
∴x(x﹣2)=0,
则x=0或x=2;
(2)解:∵∠BAC=90°,AB=5,AC=12,
∴BC= ![]() =
= ![]() =13,
=13,
∵四边形ABB′A′为菱形,
∴BB′=AB=5,
则B′C=BC﹣BB′=13﹣5=8.
【解析】(1)因式分解法求解可得;(2)根据勾股定理求得BC=13,根据菱形的性质得BB′=5,即可得答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲同学用图3-①所示的方法作出了点C,表示数
 ,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.(1)请说明甲同学这样做的理由;
(2)仿照甲同学的作法,在图3-②所给的数轴上描出表示-
 的点A.
的点A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCED的内部时,∠A、∠1、∠2之间的关系是( )
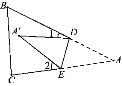
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2
C. 3∠A=∠1+∠2 D. 4∠A=∠1+∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为s时,△ADP是等腰三角形.

-
科目: 来源: 题型:
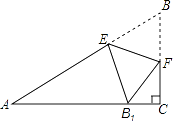
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1=________________,∠2=________________;
(2)请观察∠1、∠2分别与∠ABC有怎样的关系,归纳出一个命题.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?

相关试题

