【题目】如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为s时,△ADP是等腰三角形. 
参考答案:
【答案】![]() 或3或
或3或 ![]()
【解析】解:∵∠ABC=90°,∠A=30°,BC=2cm, ∴AC=2BC=4cm,AB=ACcosA=4× ![]() =2
=2 ![]() cm,
cm,
设运动时间为t,则AP=3t,BQ=t,
①当PA=PD时,如图1,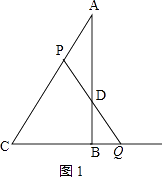
则∠BDQ=∠PDA=∠A=30°,
∴∠C=∠CPQ=60°,DQ=2BQ=2t,
∴PQ=PC=AC﹣AP=4﹣3t,
∴PD=PQ﹣DQ=4﹣3t﹣2t=4﹣5t,
则4﹣5t=3t,
解得:t= ![]() ;
;
②当AP=AD时,如图2,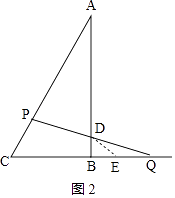
则∠ADP=∠BDQ= ![]() =75°,
=75°,
∴∠DQB=15°,
以DQ为边在∠BDQ内部作∠EDQ=∠DQB=15°,
∴设DE=QE=x,∠DEB=30°,
∴BE=BQ﹣EQ=t﹣x,
由cos∠DEB= ![]() 得
得 ![]() ,
,
解得:x=2(2﹣ ![]() )t,即DE=2(2﹣
)t,即DE=2(2﹣ ![]() )t,
)t,
∴BD=DEsin∠DEB=(2﹣ ![]() )t,
)t,
∴AD=AB﹣BD=2 ![]() ﹣(2﹣
﹣(2﹣ ![]() )t,
)t,
由AP=AD得3t=2 ![]() ﹣(2﹣
﹣(2﹣ ![]() )t,
)t,
解得:t= ![]() ;
;
③当DA=DP时,如图3,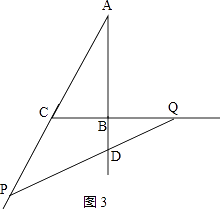
则∠A=∠APD=30°,
∴∠CQP=∠ACB﹣∠APD=30°,
∴∠CQP=∠APD=30°,
∴CP=CQ,则3t﹣4=2+t,
解得:t=3,
综上,当运动时间为 ![]() 或3或
或3或 ![]() s时,△ADP是等腰三角形.
s时,△ADP是等腰三角形.
【考点精析】本题主要考查了等腰三角形的判定的相关知识点,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题.
-
科目: 来源: 题型:
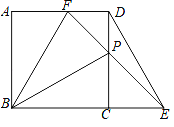
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP=x,△PBF的面积为S1,△PDE的面积为S2
(1)求证:BP⊥DE;
(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围;
(3)当∠PBF=30°时,求S1﹣S2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲同学用图3-①所示的方法作出了点C,表示数
 ,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.(1)请说明甲同学这样做的理由;
(2)仿照甲同学的作法,在图3-②所给的数轴上描出表示-
 的点A.
的点A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCED的内部时,∠A、∠1、∠2之间的关系是( )
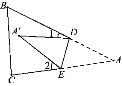
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2
C. 3∠A=∠1+∠2 D. 4∠A=∠1+∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解方程:x2=2x.
(2)如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC向右平移至△A′B′C′的位置,使得四边形ABB′A′为菱形,求B′C的长.
-
科目: 来源: 题型:
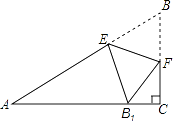
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1=________________,∠2=________________;
(2)请观察∠1、∠2分别与∠ABC有怎样的关系,归纳出一个命题.

相关试题

