搜索
【题目】甲同学用图3-①所示的方法作出了点C，表示数
，在△OAB中，∠OAB=90°，OA=2，AB=3，且点O，A，C在同一数轴上，OB=OC.
(1)请说明甲同学这样做的理由；
(2)仿照甲同学的作法，在图3-②所给的数轴上描出表示-
的点A．
参考答案：
【答案】(1) 详见解析;(2)详见解析.
【解析】
（1）根据勾股定理求得OB=
，所以点C表示的数为；
（2）如图，取OB=5，作BC⊥OB，取BC=2，根据勾股定理OC=
，所以点A表示的数为-.
解：（1）在Rt△AOB中，OB=
=
=，
因为OB=OC，所以OC=，
所以点C表示的数为；
（2）如图所示：
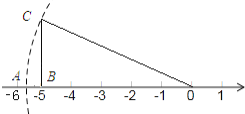
取OB=5，作BC⊥OB，取BC=2，
由勾股定理得OC=
=，
因为OA=OC=，
所以点A表示的数为-．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示平面内，有一靠在墙面上的梯子AB（粗细忽略不计），因外界因素导致梯子底端A持续向右滑动，直至整架梯子完全滑落到地面（即B与O重合），设A向右滑动的距离为x（cm），梯子的中点M与墙角O之间的距离为y（cm），则在整个滑动过程中，y与x的关系大致可表达为下列图象中的（ ）
A.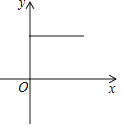
B.
C.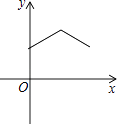
D.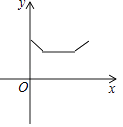
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是△ABC的边BC的中线，E是AD的中点，过点A作AF∥BC，交BE的延长线于点F，连接CF，BF交AC于G．
（1）若四边形ADCF是菱形，试证明△ABC是直角三角形；
（2）求证：CG=2AG．
-
科目： 来源： 题型：
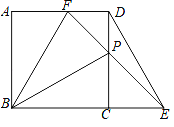
查看答案和解析>>【题目】如图，在正方形ABCD中，AB=4，P是CD边上的动点（P点不与C、D重合），过点P作直线与BC的延长线交于点E，与AD交于点F，且CP=CE，连接DE、BP、BF，设CP=x，△PBF的面积为S1，△PDE的面积为S2
（1）求证：BP⊥DE；
（2）求S1﹣S2关于x的函数解析式，并写出x的取值范围；
（3）当∠PBF=30°时，求S1﹣S2的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把一张三角形纸片沿DE折叠，当点A落在四边形BCED的内部时，∠A、∠1、∠2之间的关系是( )
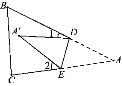
A. ∠A＝∠1＋∠2 B. 2∠A＝∠1＋∠2
C. 3∠A＝∠1＋∠2 D. 4∠A＝∠1＋∠2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中∠ABC=90°，∠A=30°，BC=2cm，动点P以3cm/s的速度由A沿射线AC方向运动，动点Q同时以1cm/s的速度由B向CB的延长线方向运动，连PQ交直线AB于D，则当运动时间为s时，△ADP是等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
（1）解方程：x2=2x．
（2）如图，Rt△ABC中，∠BAC=90°，AB=5，AC=12，将△ABC向右平移至△A′B′C′的位置，使得四边形ABB′A′为菱形，求B′C的长．
相关试题
