【题目】已知![]() ,其角平分线为
,其角平分线为![]() ,
,![]() ,其角平分线为
,其角平分线为![]() ,则
,则![]() ____.
____.
参考答案:
【答案】20°或40°
【解析】
分OC在∠AOB外部和内部两种情况,由OM、ON分别平分∠AOB、∠BOC可得∠BOM、∠BON度数,在根据两种位置分别求之.
解:①如图,当OC在∠AOB外部时,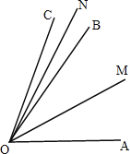
∵∠AOB=60°,OM平分∠AOB,
∴∠BOM=![]() ∠AOB=30°,
∠AOB=30°,
又∵∠BOC=20°,ON平分∠BOC,
∴∠BON=![]() ∠BOC=10°,
∠BOC=10°,
∴∠MON=∠BOM+∠BON=40°;
②如图,当OC在∠AOB内部时,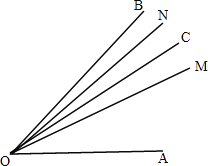
∵∠AOB=60°,OM平分∠AOB,
∴∠BOM=![]() ∠AOB=30°,
∠AOB=30°,
又∵∠BOC=20°,ON平分∠BOC,
∴∠BON=![]() ∠BOC=10°,
∠BOC=10°,
∴∠MON=∠BOM-∠BON=20°,
故答案为:40°或20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程招标时,接到甲.乙两工程队的投标书,每施工一天,需付甲工程队工程款1.5万元,乙工程队工程款1.1万元.目前有三种施工方案:
方案一:甲队单独完成此项工程刚好如期完成;
方案二:乙队单独完成此项工程比规定日期多5天;
方案三:若甲.乙两队合作4天,剩下的工程由乙队单独做也正好如期完成.
哪一种方案既能如期完工又最节省工程款?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据:
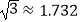 )
)
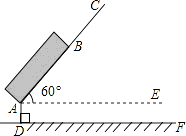
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一副直角三角板如图①放置(其中
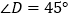 ,
,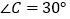 ),
),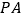 、
、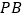 与直线
与直线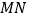 重合,且三角板
重合,且三角板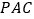 ,三角板
,三角板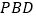 均可以绕点
均可以绕点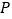 逆时针旋转.
逆时针旋转.(l)直接写出
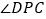 等于多少度.
等于多少度.(2)如图②,若三角板
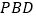 保持不动,三角板
保持不动,三角板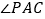 绕点
绕点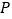 逆时针旋转,转速为
逆时针旋转,转速为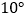 /秒,转动一周三角板
/秒,转动一周三角板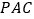 就停止转动,在旋转的过程中,当旋转时间为多少时,有
就停止转动,在旋转的过程中,当旋转时间为多少时,有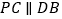 成立.
成立.(3)如图③,在图①基础上,若三角板
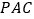 的边
的边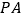 从
从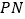 .处开始绕点
.处开始绕点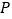 逆时针旋转,转速为
逆时针旋转,转速为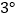 /秒,同时三角板
/秒,同时三角板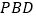 的边
的边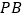 从
从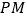 处开始绕点
处开始绕点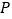 逆时针旋转,转速为
逆时针旋转,转速为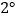 /秒,(当
/秒,(当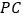 转到与
转到与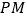 重合时,两三角板都停止转动),在旋转过程中,当
重合时,两三角板都停止转动),在旋转过程中,当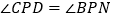 ,求旋转的时间是多少?
,求旋转的时间是多少?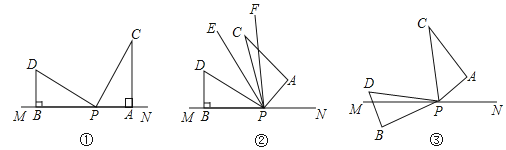
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵
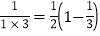 ,
,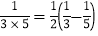 ,
,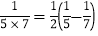 ,……
,……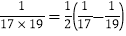 ,
,∴
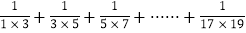
=
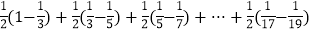
=
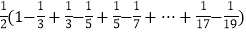 =
=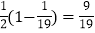 .
.解答下列问题:
(1)在和式
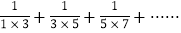 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.(2)上述求和的想法是通过逆用分式减法法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项的和为_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
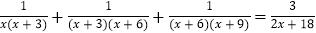 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:a+
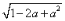 ,其中a=1007.如图是小亮和小芳的解答过程.
,其中a=1007.如图是小亮和小芳的解答过程.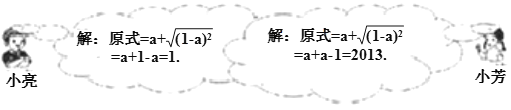
(1)_________的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:_________;
(3)先化简,再求值:a+2
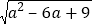 ,其中a=-2007.
,其中a=-2007.
相关试题

