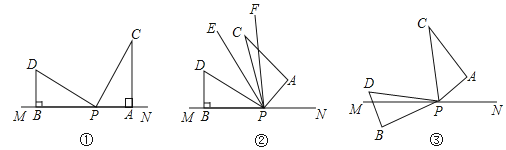
【题目】如图,有一副直角三角板如图①放置(其中![]() ,
,![]() ),
),![]() 、
、![]() 与直线
与直线![]() 重合,且三角板
重合,且三角板![]() ,三角板
,三角板![]() 均可以绕点
均可以绕点![]() 逆时针旋转.
逆时针旋转.
(l)直接写出![]() 等于多少度.
等于多少度.
(2)如图②,若三角板![]() 保持不动,三角板
保持不动,三角板![]() 绕点
绕点![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,转动一周三角板
/秒,转动一周三角板![]() 就停止转动,在旋转的过程中,当旋转时间为多少时,有
就停止转动,在旋转的过程中,当旋转时间为多少时,有![]() 成立.
成立.
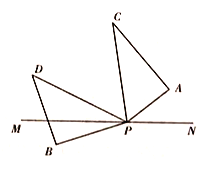
(3)如图③,在图①基础上,若三角板![]() 的边
的边![]() 从
从![]() .处开始绕点
.处开始绕点![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,同时三角板
/秒,同时三角板![]() 的边
的边![]() 从
从![]() 处开始绕点
处开始绕点![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,(当
/秒,(当![]() 转到与
转到与![]() 重合时,两三角板都停止转动),在旋转过程中,当
重合时,两三角板都停止转动),在旋转过程中,当![]() ,求旋转的时间是多少?
,求旋转的时间是多少?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() (3)
(3)![]() .
.
【解析】
(1)根据![]() 计算即可;
计算即可;
(2)分边PC在直线MN上方和下方两种情况进行讨论即可;
(3)设运动时间为t秒,![]() ,
,![]() ,根据题意用t表示出∠CPD和∠BPN的度数即可得出答案.
,根据题意用t表示出∠CPD和∠BPN的度数即可得出答案.
(1)∵一副直角三角板![]() ,
,![]()
∴![]() ,
,![]()
∴![]() =
=![]()
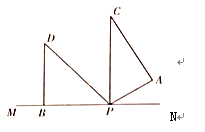
(2)第一种情况:当边PC在直线MN上方时,
如图所示,此时![]() 成立,
成立,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵三角板![]() 的转速为
的转速为![]() /秒,
/秒,
∴旋转时间为![]() .
.
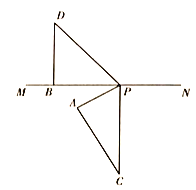
第二种情况:边PC在直线MN下方时,
如图所示,此时![]() 成立,
成立,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴三角板![]() 旋转的角度是
旋转的角度是![]() .
.
∵三角板![]() 的转速为
的转速为![]() /秒,
/秒,
∴旋转时间为![]() .
.
综上所述,当旋转时间为![]() 和
和![]() 时,有
时,有![]() 成立.
成立.
(3)设旋转的时间是![]() 秒,
秒,
由题知,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
∵![]() ,
,
∴![]() .
.
解得![]() ,
,
∴当![]() 时,旋转的时间为
时,旋转的时间为![]() .
.
-
科目: 来源: 题型:
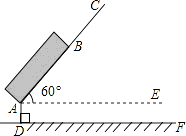
查看答案和解析>>【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据:
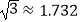 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
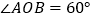 ,其角平分线为
,其角平分线为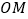 ,
, ,其角平分线为
,其角平分线为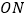 ,则
,则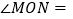 ____.
____. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵
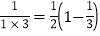 ,
,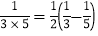 ,
,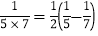 ,……
,……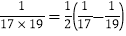 ,
,∴
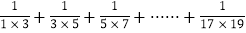
=
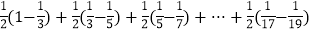
=
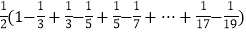 =
=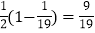 .
.解答下列问题:
(1)在和式
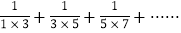 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.(2)上述求和的想法是通过逆用分式减法法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项的和为_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
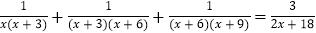 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:a+
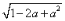 ,其中a=1007.如图是小亮和小芳的解答过程.
,其中a=1007.如图是小亮和小芳的解答过程.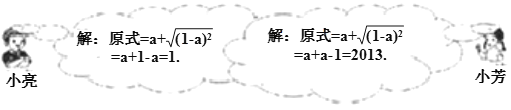
(1)_________的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:_________;
(3)先化简,再求值:a+2
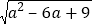 ,其中a=-2007.
,其中a=-2007. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 , 点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2 , 则当x=-3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3 . 设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
相关试题

