【题目】某文具店购进![]() 、
、![]() 两种文具进行销售.若每个
两种文具进行销售.若每个![]() 种文具的进价比每个
种文具的进价比每个![]() 种文具的进价少2元,且用900元正好可以购进50个
种文具的进价少2元,且用900元正好可以购进50个![]() 种文具和50个
种文具和50个![]() 种文具,
种文具,
(1)求每个![]() 种文具和
种文具和![]() 种文具的进价分别为多少元?
种文具的进价分别为多少元?
(2)若该文具店购进![]() 种文具的数量比购进
种文具的数量比购进![]() 种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个
种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个![]() 种文具的销售价格为12元,每个
种文具的销售价格为12元,每个![]() 种文具的销售价格为15元,则将购进的
种文具的销售价格为15元,则将购进的![]() 、
、![]() 两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进
两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进![]() 、
、![]() 两种文具有哪几种方案?
两种文具有哪几种方案?
参考答案:
【答案】(1)每个![]() 种文具的进价为8元,每个
种文具的进价为8元,每个![]() 种文具的进价为10元;(2)该五金商店有两种进货方案:①购进
种文具的进价为10元;(2)该五金商店有两种进货方案:①购进![]() 种文具67个,
种文具67个,![]() 种文具24个;②购进
种文具24个;②购进![]() 种文具70个,
种文具70个,![]() 种文具25个.
种文具25个.
【解析】
(1)设每个![]() 种文具的进价为
种文具的进价为![]() 元,每个
元,每个![]() 种文具的进价为
种文具的进价为![]() 元,根据“每个
元,根据“每个![]() 种文具的进价比每个
种文具的进价比每个![]() 种文具的进价少2元,且用900元正好可以购进50个
种文具的进价少2元,且用900元正好可以购进50个![]() 种文具和50个
种文具和50个![]() 种文具”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
种文具”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进![]() 种文具
种文具![]() 个,则购进
个,则购进![]() 种文具
种文具![]() 个,根据购进两种文具的总数量不超过95个且销售两种文具的总利润超过371元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数即可得出各进货方案.
个,根据购进两种文具的总数量不超过95个且销售两种文具的总利润超过371元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数即可得出各进货方案.
解:(1)设每个![]() 种文具的进价为
种文具的进价为![]() 元,每个
元,每个![]() 种文具的进价为
种文具的进价为![]() 元,依题意,得:
元,依题意,得:
![]() 解得:
解得:![]() .
.
答:每个![]() 种文具的进价为8元,每个
种文具的进价为8元,每个![]() 种文具的进价为10元;
种文具的进价为10元;
(2)设购进![]() 种文具
种文具![]() 个,则购进
个,则购进![]() 种文具
种文具![]() 个,依题意,得:
个,依题意,得:
![]()
解得:![]() .
.
∵![]() 为整数,
为整数,
∴![]() 或25,
或25,![]() 或70,
或70,
∴该五金商店有两种进货方案:①购进![]() 种文具67个,
种文具67个,![]() 种文具24个;②购进
种文具24个;②购进![]() 种文具70个,
种文具70个,![]() 种文具25个.
种文具25个.
故答案为:(1)每个![]() 种文具的进价为8元,每个
种文具的进价为8元,每个![]() 种文具的进价为10元;(2)该五金商店有两种进货方案:①购进
种文具的进价为10元;(2)该五金商店有两种进货方案:①购进![]() 种文具67个,
种文具67个,![]() 种文具24个;②购进
种文具24个;②购进![]() 种文具70个,
种文具70个,![]() 种文具25个.
种文具25个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
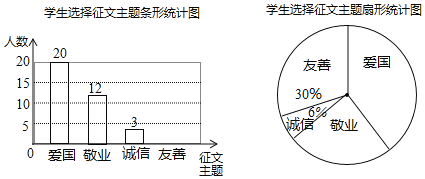
(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少度?
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)求二月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型每台进价为3500元,乙型每台进价为4000元,预计用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)对于(2)中刚进货的20台两种型号的手机,该店计划对甲型号手机在二月份售价基础上每售出一台甲型手机再返还顾客现金a元,乙型手机按销售价4400元销售,若要使(2)中所有方案获利相同,a应取何值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )

A. 4 B.
 C.
C.  D. 30
D. 30 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 轴正半轴上一动点,
轴正半轴上一动点,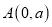 ,
, ,且
,且 、
、 满足
满足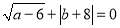 ,
, .
.
(1)求
 的面积;
的面积;(2)若
 ,
, 、
、 为线段
为线段 上的动点,作
上的动点,作 交
交 于
于 ,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB=
,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB= ,求∠BAC(用
,求∠BAC(用 表示);
表示);(3)若
 ,
, 轴于
轴于 ,点
,点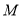 从
从 点出发,在射线
点出发,在射线 上运动,同时另一动点
上运动,同时另一动点 从点
从点 向
向 点运动,到
点运动,到 停止运动,
停止运动, 、
、 的速度分别为2个单位/秒、3个单位/秒,当
的速度分别为2个单位/秒、3个单位/秒,当 时,求运动的时间.
时,求运动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )
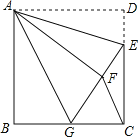
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣
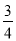 x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求
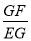 的值.
的值.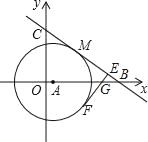
相关试题

