搜索
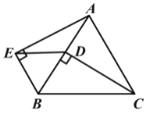
【题目】如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE.
求证:(1)△BCD≌△BAE;(2)△EBD是等边三角形.
参考答案：
【答案】(1)见解析;(2)见解析.
【解析】
（1）根据HL即可证明△BCD≌△BAE；
（2）根据等腰三角形的性质得到D为AB中点，再利用直角三角形斜边上的中线等于斜边的一半得到DE=BD，再根据等边三角形的判定定理即可求解.
证明：（1）∵△ABC是等边三角形
∴AB=BC
∵CD⊥AB,∠AEB=90°
∴∠CDB=∠AEB=90°
在Rt△BCD和Rt△BAE中，
∴△BCD≌△BAE
（2）∵△ABC是等边三角形,CD⊥AB
∴D为AB中点
∴ED=
AB=DB
∵△BCD≌△BAE
∴∠EBD=∠DBC=60°
∴△EBD是等边三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c(a≠0)经过A（-1，0），B（3，0），C（0，3）三点，其顶点为D，连接BD，点是线段BD上一个动点（不与B、D重合），过点P作y轴的垂线，垂足为E，连接BE．
（1）求抛物线的解析式，并写出顶点D的坐标；
（2）如果P点的坐标为（x，y），△PBE的面积为，求S与x的函数关系式，写出自变量x的取值范围，并求出S的最大值；
（3）在（2）的条件下，当S取得最大值时，过点P作x的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为P′，请直接写出P′点坐标，并判断点P′是否在该抛物线上．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，又继续航行7海里后，在B处测得小岛P的方位是北偏东60°，求：
（1）此时轮船与小岛P的距离BP是多少海里；
（2）小岛点P方圆3海里内有暗礁，如果轮船继续向东行使，请问轮船有没有触焦的危险？请说明理由.
-
科目： 来源： 题型：
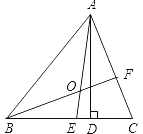
查看答案和解析>>【题目】如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=80°，∠C=54°，求∠DAC、∠BOA的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在半径为6cm的⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且∠D＝30°，下列四个结论：①OA⊥BC；②BC＝6
cm；③sin∠AOB＝
；④四边形ABOC是菱形．其中正确结论的序号是（ ）
A. ①③ B. ①②③④ C. ②③④ D. ①③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知动点A在函数y=
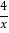（x＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC，直线DE分别交x轴，y轴于点P，Q，当QE：DP=9：25时，图中的阴影部分的面积等于___．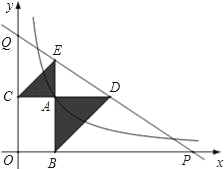
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF＝90°.求证：BE＝CF.
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH＝90°, EF＝4.求GH的长.
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上，EF,GH交于点O,∠FOH＝90°,EF＝4. 直接写出下列两题的答案：
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长；
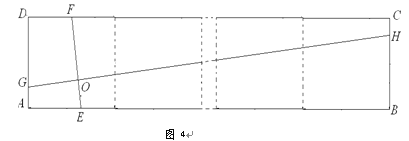
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
相关试题
