【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,其顶点为D,连接BD,点是线段BD上一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PBE的面积为,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,过点P作x的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为P′,请直接写出P′点坐标,并判断点P′是否在该抛物线上.

参考答案:
【答案】(1)顶点D的坐标为(1,4);(2)当![]() 时, S取得最大值,最大值为
时, S取得最大值,最大值为![]() ;(3)把P′坐标(
;(3)把P′坐标(![]() )代入抛物线解析式,不成立,所以
)代入抛物线解析式,不成立,所以![]() 不在抛物线上.
不在抛物线上.
【解析】
(1)根据A,B,C三点的坐标,可以运用交点式法求得抛物线的解析式.再根据顶点的坐标公式求得抛物线的顶点坐标;
(2)根据B,D的坐标运用待定系数法求得直线BD的解析式,再根据三角形的面积公式以及y与x之间的函数关系式得到s与x之间的函数关系式.点P的横坐标即x的值位于点D和点B的横坐标之间.根据二次函数的顶点式即可分析其最值;
(3)根据(2)中的坐标得点E和点C重合.过P′作P′H⊥y轴于H,P′F交y轴于点M.要求P′H和OH的长.P′H的长可以运用直角三角形P′CM的面积进行计算.设MC=m,则MF=m,P′M=3m,P′E=32.根据勾股定理列方程求解,得到直角三角形P′CM的三边后,再根据直角三角形的面积公式进行计算.要求OH的长,已知点C的坐标,只需根据勾股定理进一步求得CH的长即可.把求得的点P的坐标代入抛物线解析式即可判断点P′是否在该抛物线上.
(1)设![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
∴抛物线的解析式为:![]() ,
,
顶点![]() 的坐标为
的坐标为![]() ;
;
(2)设直线![]() 解析式为:
解析式为:![]() (
(![]() ),把
),把![]() 两点坐标代入,
两点坐标代入,
得![]()
解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() ;
;
(3)当![]() 取得最大值,
取得最大值,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,
,
法一:过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,
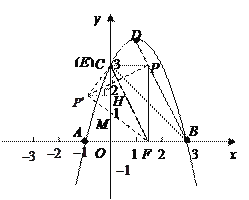
设![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理,
中,由勾股定理,
![]() ,
,
解得![]() ,
,
∵![]() ,
,
∴![]() ,
,
由![]() ,可得
,可得![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 坐标
坐标![]() ;
;
法二:连接![]() ,交
,交![]() 于点
于点![]() ,分别过点
,分别过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
易证![]() ,
,
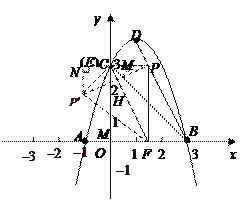
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
由三角形中位线定理,
![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,
,
∴![]() 坐标
坐标![]() .
.
把![]() 坐标
坐标![]() 代入抛物线解析式,不成立,所以
代入抛物线解析式,不成立,所以![]() 不在抛物线上.
不在抛物线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元?
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>0)支钢笔需要花y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据:
 ,
, ,
, ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,求:
(1)此时轮船与小岛P的距离BP是多少海里;
(2)小岛点P方圆3海里内有暗礁,如果轮船继续向东行使,请问轮船有没有触焦的危险?请说明理由.

-
科目: 来源: 题型:
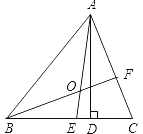
查看答案和解析>>【题目】如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=80°,∠C=54°,求∠DAC、∠BOA的度数.
-
科目: 来源: 题型:
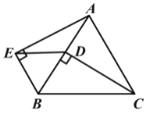
查看答案和解析>>【题目】如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE.
求证:(1)△BCD≌△BAE;(2)△EBD是等边三角形.
相关试题

