【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

参考答案:
【答案】(1)5;(2)(0,﹣5);(3) (0, ![]() )或(0,﹣2).
)或(0,﹣2).
【解析】试题解析:(1)延长AB交y轴于P点,如图,利用待定系数法求出直线AB的解析式为y=-x-5,则得到P(0,-5),然后根据三角形面积公式和利用S△OAB=S△AOP-S△OBP进行计算即可;
(2)由(1)得到P点的坐标;
(3)分类讨论:当Q在y轴的正半轴上时,利用S四边形ABOQ=S△AOB+S△AOQ得到S△AOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标;当Q在y轴的负半轴上时,利用S四边形ABOQ=S△AOB+S△BOQ得到S△BOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标.
试题解析:(1)延长AB交y轴于P点,如图,

设直线AB的解析式为y=kx+b,
把A(﹣3,﹣2)、B(﹣1,﹣4)代入得![]()
解得![]() .
.
所以直线AB的解析式为y=﹣x﹣5,
当x=0时,y=﹣x﹣5=﹣5,则P(0,﹣5),
所以S△OAB=S△AOP﹣S△OBP
=![]() ×5×3﹣
×5×3﹣![]() ×5×1
×5×1
=5.
(2)由(1)得到P点的坐标为(0,﹣5);
(3)当Q在y轴的正半轴上时,∵S四边形ABOQ=S△AOB+S△AOQ,
∴S△AOQ=6﹣5=1,
∴![]() ×3×OQ=1,
×3×OQ=1,
解得OQ=![]() .
.
则此时Q点的坐标为(0, ![]() );
);
当Q在y轴的负半轴上时,
∵S四边形ABOQ=S△AOB+S△BOQ,
∴S△BOQ=1,
∴S△AOQ=6﹣5=1,
∴![]() ×1×OQ=1,
×1×OQ=1,
解得OQ=2,
则此时Q点的坐标为(0,﹣2),
即Q点坐标为(0, ![]() )或(0,﹣2).
)或(0,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表回答问题:
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
x2
256
259.21
262.44
265.69
268.96
272.25
175.56
278.89
282.24
(1)272.25的平方根是
(2)
 = ,
= ,  = ,
= ,  =
= (3)设
 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根
 .
.(1)求实数k的取值范围.
(2)若方程两实根
 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

-
科目: 来源: 题型:
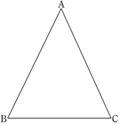
查看答案和解析>>【题目】如图所示,在△ABC中,∠ABC=∠ACB.
(1)尺规作图:过顶点A,作△ABC的角平分线AD;(不写作法,保留作图痕迹)
(2)在AD上任取一点E,连接BE、CE.求证:BE=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
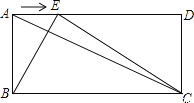
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 ; (2)
; (2)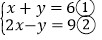 ;
;(3)
 ; (4)
; (4)
相关试题

