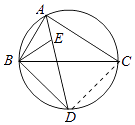
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
参考答案:
【答案】
(1)证明:∵BE平分∠BAC,AD平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴ ![]() ,
,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB
(2)解:连接CD,如图所示:
由(1)得: ![]() ,
,
∴CD=BD=4,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC= ![]() =4
=4 ![]() ,
,
∴△ABC外接圆的半径= ![]() ×4
×4 ![]() =2
=2 ![]() .
.
【解析】(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出 ![]() ,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得:
,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得: ![]() ,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC=
,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC= ![]() =4
=4 ![]() ,即可得出△ABC外接圆的半径.
,即可得出△ABC外接圆的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④
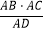 为常量.其中正确的有 .
为常量.其中正确的有 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,第一秒它从原点跳动到点(0,1),第二秒它从点(0,1)跳到点(1,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],每秒跳动一个单位长度,那么30秒后跳蚤所在位置的坐标是___.
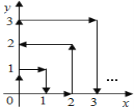
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
① +
+  ﹣
﹣  =
=  ;
;
② +
+  ﹣
﹣ 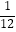 =
=  ;
;
③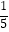 +
+  ﹣
﹣ 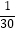 =
=  ;
;
④ +
+  ﹣
﹣  =
=  ;
;
…
(1)请按以上规律写出第⑤个等式:;
(2)猜想并写出第n个等式:;
(3)请证明猜想的正确性. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
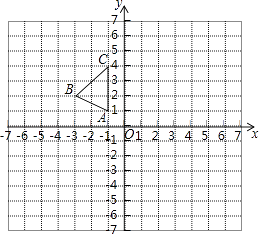
①画出与△ABC关于y轴对称的△A1B1C1 , 求点C1的坐标。
②以原点O为位似中心,在第四象限画一个△A2B2C2 , 使它与△ABC位似,并且△A2B2C2与△ABC的相似比为2:1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
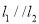 ,直线
,直线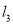 与直线
与直线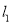 、
、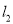 分别相交于C、D两点.
分别相交于C、D两点.(1)如图a,有一动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
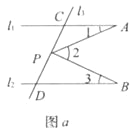
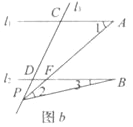
(2)如图b,当动点P线段CD之外运动(不与C、D两点重合),问上述结论是否成立?若不成立,试写出新的结论并说明理由.
相关试题

