【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4
B.1.1
C.0.8
D.0.5
参考答案:
【答案】C
【解析】解:如图,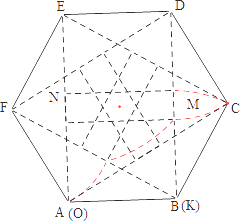
在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣ ![]() 小于等于1,
小于等于1,
所以答案是:C.
【考点精析】关于本题考查的正多边形和圆和旋转的性质,需要了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。

根据以上信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为  元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为  元,分别求出
元,分别求出  ,
,  关于
关于  的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
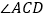 是
是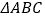 的外角,
的外角,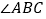 与
与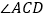 的角平分线交于点
的角平分线交于点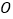 .
.(1)若
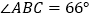 ,
,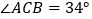 ,则
,则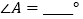 ,
,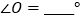 ;
;(2)探索
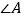 与
与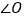 的数量关系,并说明理由;
的数量关系,并说明理由;(3)若
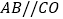 ,
,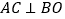 ,求
,求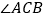 的度数.
的度数.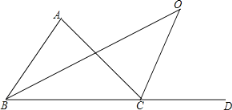
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六,小明一家共7人从某地出发去参观世博会.小明提议:让爸爸载着爷爷、奶奶、外公、外婆去,自己和妈妈从某41路车去,最后在地铁8号线某博物馆汇合,图中
 分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:
分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:
(1)某41路车在途中行驶的平均速度为 千米/分钟;此次行驶的路程是 千米;
(2)写出小轿车在行驶过程中
 与
与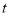 的函数关系式: ,定义域为 ;
的函数关系式: ,定义域为 ;(3)小明和妈妈乘坐的某41路出发 分钟后被爸爸的小轿车追上了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣
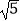 ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2 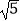 ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2 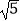 .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
相关试题

