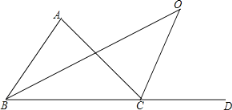
【题目】如图,![]() 是
是![]() 的外角,
的外角,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
(2)探索![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
参考答案:
【答案】(1)80、40;(2)![]() ;理由见解析;(3)
;理由见解析;(3)![]() .
.
【解析】
(1)由三角形内角和定理可求∠A,然后求出∠OBC和∠OCD,再由三角形外角的性质即可求出结论;
(2)由题中角平分线可得∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACD,根据三角形内角和定理可得∠A+∠ABO=∠O+∠ACO,又由∠ACD=∠A+∠ABC=∠A+2∠ABO,进而得出∠A+∠ABO=∠O+
∠ACD,根据三角形内角和定理可得∠A+∠ABO=∠O+∠ACO,又由∠ACD=∠A+∠ABC=∠A+2∠ABO,进而得出∠A+∠ABO=∠O+![]() ∠A+∠ABO,即可得出结论;
∠A+∠ABO,即可得出结论;
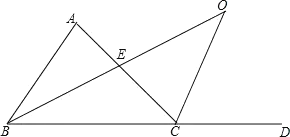
(3)AC与BO交于点E,由OC∥AB,证得∠ABO=∠O,由AC⊥BO,证得∠AEB=90°,故2∠O+∠O=90°,进而证得∠A=60°,由∠ABC=2∠ABO即可证得结论.
设![]() 与
与![]() 交于点
交于点![]()
解:(1)![]() ,
,![]() ,
,![]() ,
,
![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
故答案为:80、40;
(2)∵BO平分∠ABC,
∴∠ABO=![]() ∠ABC,
∠ABC,
∵CO平分∠ACD,
∴∠ACO=![]() ∠ACD,
∠ACD,
∵∠AEB=∠CEO,
∴∠A+∠ABO=∠O+∠ACO,
∴∠A+∠ABO=∠O+![]() ∠ACD,
∠ACD,
∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC=∠A+2∠ABO,
∴∠A+∠ABO=∠O+![]() ∠A+∠ABO,
∠A+∠ABO,
∴![]() ∠A=∠O;
∠A=∠O;
(3)如图,![]() 与
与![]() 交于点
交于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d=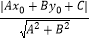 .
.
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d=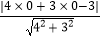 =
= 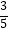 .
.
根据以上材料,解决下列问题:
(1)点P1(3,4)到直线y=﹣ x+
x+  的距离为;
的距离为;
(2)已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣ x+b相切,求实数b的值;
x+b相切,求实数b的值;
(3)如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。

根据以上信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为  元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为  元,分别求出
元,分别求出  ,
,  关于
关于  的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4
B.1.1
C.0.8
D.0.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】上周六,小明一家共7人从某地出发去参观世博会.小明提议:让爸爸载着爷爷、奶奶、外公、外婆去,自己和妈妈从某41路车去,最后在地铁8号线某博物馆汇合,图中
 分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:
分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:
(1)某41路车在途中行驶的平均速度为 千米/分钟;此次行驶的路程是 千米;
(2)写出小轿车在行驶过程中
 与
与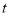 的函数关系式: ,定义域为 ;
的函数关系式: ,定义域为 ;(3)小明和妈妈乘坐的某41路出发 分钟后被爸爸的小轿车追上了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
相关试题

