【题目】如图,在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:
(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②说明理由.
(2)三角板绕点P旋转,△PCE是否能成为等腰三角形?若能,指出所有情况(即写出△PCE为等腰三角形时BE的长);若不能,请说明理由.

参考答案:
【答案】(1)PD=PE,理由见解析;(2)BE=0,2-![]() ,2+
,2+![]() 或1.
或1.
【解析】
(1)PD=PE,通过证△DPC≌△EPB,可得结论
(2)分三种情况讨论①当PC=PE=![]() 时;②当PC=CE=
时;②当PC=CE=![]() 时;③当PE=EC时,可求解.
时;③当PE=EC时,可求解.
解:(1)PD=PE
如图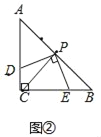
连接PB
∵△ABC是等腰直角三角形,P是AB中点
∴CP⊥AB,∠ACP=∠BCP=![]() ∠ACB=45°
∠ACB=45°
∴∠ACP=∠B=∠BCP=45°
∴BP=CP
∵∠DPC+∠CPE=90°=∠BPE+∠CPE
∴∠DPC=∠EPB,BP=CP,∠ACP=∠B
∴△DPC≌△EPB
∴DP=PE
(2)∵AC=BC=2,∠C=90°
∴AB=2![]()
∴AP=BP=CP=![]()
△PCE是等腰三角形
当PC=PE=![]() 时,即B,E重合,BE=0
时,即B,E重合,BE=0
当PC=CE=![]() 时,E在线段BC上,则BE=2﹣
时,E在线段BC上,则BE=2﹣![]()
E在线段BC的延长线上,则BE=2+![]()
当PE=EC,且∠PCB=45°
∴∠PEC=90°
∴EC=1
∴BE=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)

若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列各题:
(1)解不等式﹣x+1<7x﹣3;
(2)解不等式
 ;
;(3)解不等式
 ,并把它的解集表示在数轴上.
,并把它的解集表示在数轴上.(4)已知关于x的不等式组
 ,恰好有两个整数解,试确定实数a的取值范围.
,恰好有两个整数解,试确定实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:(1)-3+(-2)+4;(2)10÷
 ×(-6);(3)99
×(-6);(3)99 ×(-8);(4)-14+(-2)3÷4×[5-(-3)2].
×(-8);(4)-14+(-2)3÷4×[5-(-3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a,b的多项式2(a2-2ab-b2)-(a2+mab+2b2).
(1)若合并后不含有ab项,求m的值;
(2)在(1)的条件下,当a=-3,b=
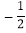 时,求代数式的值.
时,求代数式的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一条直线上从左往右依次有A、B、C、D四个点.
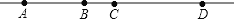
(1)如果线段AC、BC、BD的长分别为3a-b、a+b、4a-2b,试求A、D两点间的距离;
(2)如果将这条直线看作是以点C为原点的数轴(向右为正方向).
①直接写出数轴上与点B距离为a+2b的点所表示的数______;
②设线段BD上一动点P所表示的数为x,求|x+a+b|+|x-3a+3b|的值(用含a、b的代数表示);
③线段BD上有两个动点P、M,点P所表示的数为x,点M所表示的数为y,直接写出式子|x-y|+|x+a+b|+|x-y-6a+4b|的最小值______(用含a、b的代数表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从
 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
相关试题

