【题目】如图所示,一条直线上从左往右依次有A、B、C、D四个点.
![]()
(1)如果线段AC、BC、BD的长分别为3a-b、a+b、4a-2b,试求A、D两点间的距离;
(2)如果将这条直线看作是以点C为原点的数轴(向右为正方向).
①直接写出数轴上与点B距离为a+2b的点所表示的数______;
②设线段BD上一动点P所表示的数为x,求|x+a+b|+|x-3a+3b|的值(用含a、b的代数表示);
③线段BD上有两个动点P、M,点P所表示的数为x,点M所表示的数为y,直接写出式子|x-y|+|x+a+b|+|x-y-6a+4b|的最小值______(用含a、b的代数表示).
参考答案:
【答案】(1)6a-4b;(2)①b或-2a-3b;②4a-2b;③6a-4b.
【解析】
(1)根据线段的和差计算即可;
(2)①先根据题意表示出点B的坐标,再分所求点在点B的左右两种情况讨论即可;
②根据题意可知x>-a-b,进而得出x+a+b>0,由题意可得x<3a-3b,进而得出x-3a+3b<0,进一步求解即可;
③由AD的长即可得出结果.
解:(1)AB=AC-BC=(3a-b)-(a+b)=3a-b-a-b=2a-2b;
∴AD=AB+BD=(2a-2b)+(4a-2b)=2a-2b+4a-2b=6a-4b;
(2)①∵点C为原点,BC=a+b,
∴点B的坐标为:-a-b,
∴数轴上与点B距离为a+2b的点所表示的数为(a+2b)+(-a-b)=b或-a-b-(a+2b)=-2a-3b.
故答案b或-2a-3b;
②x>-a-b即x+a+b>0,x<3a-3b,即x-3a+3b<0,
所以|x+a+b|+|x-3a+3b|=x+a+b-(x-3a+3b)=4a-2b;
③∵AD=6a-4b,
∴|x-y|+|x+a+b|+|x-y-6a+4b|的最小值6a-4b.
故答案为6a-4b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:(1)-3+(-2)+4;(2)10÷
 ×(-6);(3)99
×(-6);(3)99 ×(-8);(4)-14+(-2)3÷4×[5-(-3)2].
×(-8);(4)-14+(-2)3÷4×[5-(-3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:
(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②说明理由.
(2)三角板绕点P旋转,△PCE是否能成为等腰三角形?若能,指出所有情况(即写出△PCE为等腰三角形时BE的长);若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a,b的多项式2(a2-2ab-b2)-(a2+mab+2b2).
(1)若合并后不含有ab项,求m的值;
(2)在(1)的条件下,当a=-3,b=
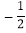 时,求代数式的值.
时,求代数式的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从
 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
 (x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比例函数图象上移动时,点B也在某一反比例函数y=
(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比例函数图象上移动时,点B也在某一反比例函数y=  图象上移动,则k的值为( )
图象上移动,则k的值为( )
A.﹣4
B.4
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号)
①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.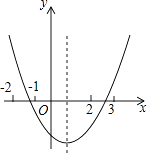
相关试题

