[题目]已知动点P以每秒2㎝的速度沿图甲的边框按从的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:(1)图甲中的BC长是多少?(2)图乙中的a是多少?(3)图甲中的图形面积的多少?(4)图乙的b是多少? 题目和参考答案 ——青夏教育精英家教网—

【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题：

(1)图甲中的BC长是多少？

(2)图乙中的a是多少?

(3)图甲中的图形面积的多少?

(4)图乙的b是多少?

参考答案：

【答案】（1）8㎝（2）24㎝2（3）60㎝2(4) 17秒

【解析】(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(㎝) (3分)

(2) a=S△ABC=×6×8=24(㎝2) (6分)

(3) 同理,由图象知 CD=4㎝,DE=6㎝,则EF=2㎝,AF=14㎝

∴图1中的图象面积为4×8+2×14=60㎝2 (9分)

(4) 图1中的多边形的周长为(14+6)×2=40㎝ b=(40－6)÷2=17秒 (12分)

（1）根据题意得：动点P在BC上运动的时间是4秒，又由动点的速度，可得BC的长；

（2）由（1）可得BC的长，又由AB=6cm，可以计算出△ABP的面积，计算可得a的值；

（3）分析图形可得，甲中的图形面积等于AB×AF-CD×DE，根据图象求出CD和DE的长，代入数据计算可得答案，

（4）计算BC+CD+DE+EF+FA的长度，又由P的速度，计算可得b的值．

相关试题

科目： 来源： 题型：

【题目】已知△ABC内接于⊙O ， AC是⊙O的直径，D是弧AB的中点．过点D作CB的垂线，分别交CB、CA延长线于点F、E ．

（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）若CF＝6，∠ACB＝60°，求阴影部分的面积．
查看答案和解析>>
科目： 来源： 题型：

【题目】宁波某公司经销一种绿茶，每千克成本为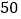元．市场调查发现，在一段时间内，销售量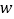（千克）随销售单价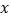（元/千克）的变化而变化，具体关系式为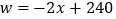：．设这种绿茶在这段时间内的销售利润为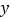（元），解答下列问题：
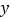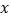（1）求与的关系式；
（2）当销售单价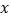取何值时，销售利润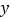的值最大，最大值为多少？
（3）如果物价部门规定这种绿茶的销售单价不得高于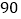元/千克，公司想要在这段时间内获得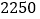元的销售利润，销售单价应定为多少元？
查看答案和解析>>
科目： 来源： 题型：

【题目】请阅读下列材料，并完成相应的任务。
阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一.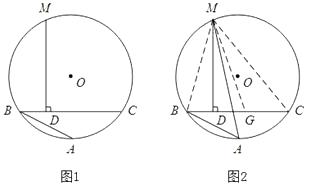

阿基米德折弦定理：如图1，AB和BC是圆O的两条弦（即折线ABC是圆的一条折弦）， BC＞AB，M是的中点，即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
证明：如图2，在CB上截取CG=AB，连接MA、MB、MC、MG。因为M是弧ABC的中点，所以MA=MC.
任务：
（1）请按照上面的证明思路，完整证明阿基米德折弦定理，即CD=AB+BD。
（2）如图3，已知等边△ABC内接于圆O，AB=1，D为上一点，∠ABD=45°，AE⊥BD于点E，则△BDC的周长是.
查看答案和解析>>
科目： 来源： 题型：

【题目】某市出租车计费方法如图所示，x（km）表示行驶里程，y（元）表示车费，请根据图象回答下面的问题：
（1）出租车的起步价是多少元？当x＞3时，求y关于x的函数关系式．
（2）若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程．
查看答案和解析>>
科目： 来源： 题型：

【题目】在长方形ABCD中，AB=3，BC=4，动点P从点A开始按A→B→C→D的方向运动到点D.如图，设动点P所经过的路程为x，△APD的面积为y.(当点P与点A或D重合时，y=0)
(1)写出y与x之间的函数解析式；
(2)画出此函数的图象．
查看答案和解析>>
科目： 来源： 题型：

【题目】如果一个三角形能被一条线段分割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形.

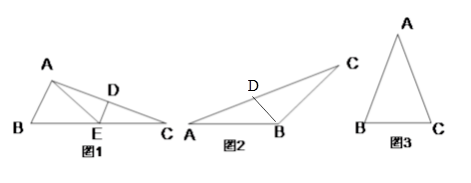
（1）如图1，△ABC中，∠B=2∠C，线段AC的垂直平分线交AC于点D，交BC于点E.
求证：AE是△ABC的一条特异线.
（2）如图2，已知BD是△ABC的一条特异线，其中∠A=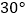 ，∠ABC为钝角，求出所有可能的∠ABC的度数.
（3）如图3，△ABC是一个腰长为2的等腰锐角三角形，且它是特异三角形，若它的顶角
度数为整数，请求出其特异线的长度；若它的顶角度数不是整数，请直接写出顶角度数.
查看答案和解析>>