【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想: .

参考答案:
【答案】(1)①=;②∠BCA=180°-∠α;(2 )EF=BE+AF.
【解析】试题分析:(1)①由∠BCA=90°,∠α=90°可得∠CBE+∠BCE=90°,∠BCE+∠ACD=90°,可推得∠CBE=∠ACD,且已知CA=CB,∠BEC=∠CFA,所以△BEC≌△CDA,可得BE=CF;
②只有满足△BEC≌△CDA,才有①中的结论,即∠BCE=∠CAF,∠CBE=∠FCA;由三角形内角和等于180°,可知∠α+∠BCE+∠CBE=180°,即∠α+∠BCE+∠FCA=180°,即可得到∠BCA=180°-∠α;
(2)只要通过条件证明△BEC≌△CFA(可通过ASA证得),可得BE=CF,EC=AF,即可得到EF=EC+CF=BE+AF.
试题解析:(1)①∵∠BCA=90°,∠α=90°,
∴∠CBE+∠BCE=90°,∠BCE+∠ACD=90°,
∴∠CBE=∠ACD,
在△BEC与△CDA中,
∵ ,
,
∴△BEC≌△CFA(AAS),
∴BE=CF
故答案为:=;
②∠α与∠BCA应满足的关系是∠BCA=180°-∠α,理由为:
∵∠α+∠BCA=180°,
∴∠α+∠BCE+∠FCA=180°,
∵∠α+∠BCE+∠CBE=180°(三角形内角和等于180°),
∴∠CBE=∠ACD,
又∵∠BEC=∠CFA,CA=CB,
∴△BEC≌△CFA(AAS),
∴BE=CF,
则∠α与∠BCA应满足的关系是∠BCA=180°-∠α;
(2)探究结论:EF=BE+AF,
∵∠1+∠2+∠BCA=180°,∠2+∠3+∠CFA=180°,
又∵∠BCA=∠α=∠CFA,
∴∠1=∠3;
又∵∠BEC=∠CFA=∠α,CB=CA,
∴△BEC≌△CFA(AAS),
∴BE=CF,EC=FA,
∴EF=EC+CF=BE+AF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程a(x+m)2+b=0(a、b、m为常数,a≠0)的解是x1=2,x2=﹣1,那么方程a(x+m+2)2+b=0的解_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).
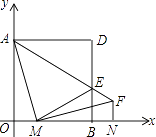
(1)直接写出点D和M的坐标(可用含t式子表示);
(2)当△MNF面积为 时,求t的值;
时,求t的值;
(3)△AME能否为等腰三角形?若不能请说明理由;若能,求出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3x2﹣x2=3
B.aa3=a3
C.a6÷a3=a2
D.(a2)3=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(a+b)(3a-2b)-b(a-b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示.
时间段(小时/周)
小丽抽样(人数)
小杰抽样(人数)
0~1
6
22
1~2
10
10
2~3
16
6
3~4
8
2
(1)你认为哪位学生抽取的样本不合理?请说明理由.
(2)专家建议每周上网2小时以上(含2小时)的学生应适当减少上网的时间,估计该校全体初二学生中有多少名学生应适当减少上网的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)(x2y+3)(x2y-3)
(3)(3mn+1)(3mn-1)-8m2n2
(4)(x+3y-2)(x-3y-2)
相关试题

