【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
参考答案:
【答案】D
【解析】
由AB=AC知∠B=∠C,据此得2∠C+∠BAC=180°,结合∠C+∠BAC=145°可知∠C=35°,根据∠DAE=90°、AD=AE知∠AED=45°,利用∠EDC=∠AED-∠C可得答案.
∵AB=AC,
∴∠B=∠C,
∴∠B+∠C+∠BAC=2∠C+∠BAC=180°,
又∵∠C+∠BAC=145°,
∴∠C=35°,
∵∠DAE=90°,AD=AE,
∴∠AED=45°,
∴∠EDC=∠AED-∠C=10°,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所给条件中,不能判断两个直角三角形全等的是( )
A. 一个锐角和这个锐角的对边对应相等B. 一个锐角与斜边对应相等
C. 两锐角对应相等D. 一锐角和一边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC中,AD⊥BC于点D,且AD=
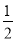 BC,则△ABC底角的度数为( )
BC,则△ABC底角的度数为( )A.45°B.75°C.45°或75°D.60°
-
科目: 来源: 题型:
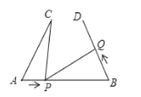
查看答案和解析>>【题目】如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA=60 ,点 P 在线段 AB 上以 1cm/s 的速度由点A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动。它们运动的时间为 t(s),则点 Q的运动速度为________cm/s,使得 A. C. P 三点构成的三角形与 B. P、Q 三点构成的三角形全等。
-
科目: 来源: 题型:
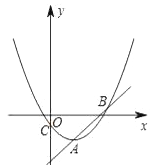
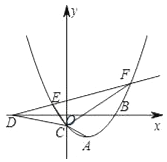
查看答案和解析>>【题目】如图,抛物线
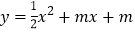 (m<0)的顶点为A,交y轴于点C.
(m<0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);
(2)平移直线y=x经过点A交抛物线C于另一点B,直线AB下方抛物线C上一点P,求点P到直线AB的最大距离
(3)设直线AC交x轴于点D,直线AC关于x轴对称的直线交抛物线C于E、F两点.若∠ECF=90°,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,已知抛物线
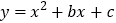 经过
经过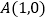 ,
,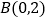 两点,顶点为
两点,顶点为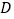 .
.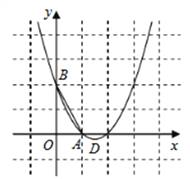
(1)求抛物线的解析式;
(2)将
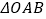 绕点
绕点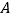 顺时针旋转
顺时针旋转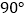 后,点
后,点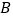 落在点
落在点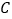 的位置,将抛物线沿
的位置,将抛物线沿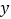 轴平移后经过点
轴平移后经过点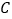 ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;(3)设(2)中平移后,所得抛物线与
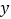 轴的交点为
轴的交点为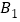 ,顶点为
,顶点为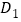 ,若点
,若点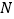 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足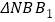 的面积是
的面积是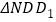 面积的2倍,求点
面积的2倍,求点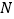 的坐标.
的坐标.
相关试题

