【题目】(题文)如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,顶点为
两点,顶点为![]() .
.
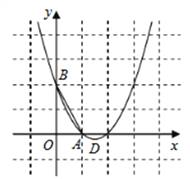
(1)求抛物线的解析式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,点
后,点![]() 落在点
落在点![]() 的位置,将抛物线沿
的位置,将抛物线沿![]() 轴平移后经过点
轴平移后经过点![]() ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)抛物线的解析式为![]() .(2)平移后的抛物线解析式为:
.(2)平移后的抛物线解析式为:![]() .(3)点
.(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】(1)利用待定系数法,将点A,B的坐标代入解析式即可求得;
(2)根据旋转的知识可得:A(1,0),B(0,2),∴OA=1,OB=2,
可得旋转后C点的坐标为(3,1),当x=3时,由y=x2-3x+2得y=2,可知抛物线y=x2-3x+2过点(3,2)∴将原抛物线沿y轴向下平移1个单位后过点C.∴平移后的抛物线解析式为:y=x2-3x+1;
(3)首先求得B1,D1的坐标,根据图形分别求得即可,要注意利用方程思想.
详解: (1)已知抛物线![]() 经过
经过![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴所求抛物线的解析式为![]() .
.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
可得旋转后![]() 点的坐标为
点的坐标为![]() .
.
当![]() 时,由
时,由![]() 得
得![]() ,
,
可知抛物线![]() 过点
过点![]() .
.
∴将原抛物线沿![]() 轴向下平移1个单位长度后过点
轴向下平移1个单位长度后过点![]() .
.
∴平移后的抛物线解析式为:![]() .
.
(3)∵点![]() 在
在![]() 上,可设
上,可设![]() 点坐标为
点坐标为![]() ,
,
将![]() 配方得
配方得![]() ,∴其对称轴为
,∴其对称轴为![]() .由题得B1(0,1).
.由题得B1(0,1).
①当![]() 时,如图①,
时,如图①,
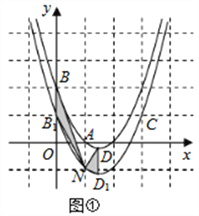
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
此时![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.
②当![]() 时,如图②,
时,如图②,
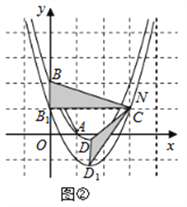
同理可得![]() ,
,
∴![]() ,
,
此时![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
-
科目: 来源: 题型:
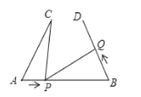
查看答案和解析>>【题目】如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA=60 ,点 P 在线段 AB 上以 1cm/s 的速度由点A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动。它们运动的时间为 t(s),则点 Q的运动速度为________cm/s,使得 A. C. P 三点构成的三角形与 B. P、Q 三点构成的三角形全等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
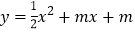 (m<0)的顶点为A,交y轴于点C.
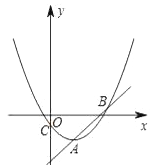
(m<0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);
(2)平移直线y=x经过点A交抛物线C于另一点B,直线AB下方抛物线C上一点P,求点P到直线AB的最大距离
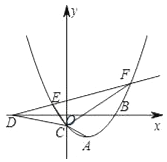
(3)设直线AC交x轴于点D,直线AC关于x轴对称的直线交抛物线C于E、F两点.若∠ECF=90°,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩种植果树.2018年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果运到市场出售平均每天售出1000千克,需8人帮忙,每人每天付工资100元,农用车运费及其他各项费用平均每天200元.若只能选择一种方式出售:
(1)分别用a,b表示两种方式出售全部水果的收入;
(2)若a=2,b=1,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式收入较高.
-
科目: 来源: 题型:
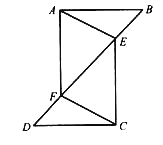
查看答案和解析>>【题目】如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
-
科目: 来源: 题型:
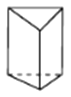
查看答案和解析>>【题目】观察下列多面体,并把下表补充完整.
名称
三棱柱
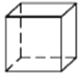
四棱柱
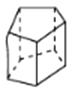
五棱柱
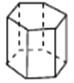
六棱柱
图形
顶点数
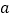
6
10
12
棱数
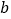
9
12
面数
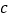
5
8
观察上表中的结果,你能发现
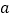 、
、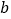 、
、之间有什么关系吗?请写出关系式.
相关试题

