【题目】已知关于x的方程2x2﹣(4k+2)x+2k2+1=0.
(1)当k取何值时,方程有两个不相等的实数根?
(2)当k取何值时,方程有两个相等的实数根?
(3)当k取何值时,方程没有实数根?
参考答案:
【答案】
(1)解:△=(4k+2)2﹣8(2k2+1)=16k﹣4;
当k> ![]() 时,方程有两个不相等的实数根
时,方程有两个不相等的实数根
(2)解:当k= ![]() 时,方程有两个相等的实数根
时,方程有两个相等的实数根
(3)解:当k< ![]() 时,方程没有实数根
时,方程没有实数根
【解析】(1)根据判别式的意义得到△=(4k+2)2﹣8(2k2+1)=16k﹣4>0,然后解不等式解即可;(2)根据判别式的意义得到△=(4k+2)2﹣8(2k2+1)=16k﹣4=0,求出k的值即可;(3)根据判别式的意义得到△=(4k+2)2﹣8(2k2+1)=16k﹣4<0,然后解不等式解即可.
【考点精析】通过灵活运用求根公式,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,△A1B1C1和△A2B2C2的顶点都在方格纸的格点上.

(1)求△A1B1C1和△A2B2C2的面积比.
(2)点A1、D、E、F、G、H是△A1B1C1边上的6个格点,请在这6个格点中选取3个点作为三角形的顶点,使构成的三角形与△A2B2C2相似(要求写出2个符合条件的三角形,并分别在图1和图2中将相应三角形涂黑,不必说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10 cm,现要在OC,OA上分别找点Q,N,使QM+QN最小,则其最小值为________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:如图①,四边形 ABCD是正方形,BE⊥BF,BE=BF,求证:△ABE≌△CBF;
方法拓展:如图②,ABCD是矩形,BC=2AB,BF⊥BE,BF=2BE,若矩形ABCD的面积为40,△ABE的面积为4,求阴影部分图形的面积.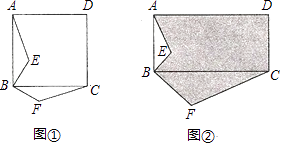
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2)

(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G为顶点的三角形相似?请说明理由.
相关试题

