【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由AB是⊙O的直径,AC为⊙![]() 切线得到∠ADB=∠BAE=90°,进而可知 ∠DAE+∠BAD=∠CDE+∠ODA=
切线得到∠ADB=∠BAE=90°,进而可知 ∠DAE+∠BAD=∠CDE+∠ODA=![]() ,由OA=OD可知∠OAD=∠ODA,进而可知∠BAE=∠CDE,∠C为公共角,即可证明△CDE∽△CAD,(2)根据勾股定理可求出OC的长,进而求出DC的长,通过△CDE∽△CAD即可求出AE的长.
,由OA=OD可知∠OAD=∠ODA,进而可知∠BAE=∠CDE,∠C为公共角,即可证明△CDE∽△CAD,(2)根据勾股定理可求出OC的长,进而求出DC的长,通过△CDE∽△CAD即可求出AE的长.
(1)∵AB为直径,AC为⊙![]() 切线,
切线,
∴∠ADB=∠BAE=![]() ,
,
∴∠DAE+∠BAD=∠CDE+∠ODA=![]() ,
,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠BAE=∠CDE,
∵∠C为公共角,
∴△CDE∽△CAD,
(2)∵AB=2,
∴AO=OD=1,
∵AC=![]() ,∠BAC=Rt∠,
,∠BAC=Rt∠,
∴![]() ,
,
∴DC=OC-OD=2,
∵△CDE∽△CAD,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A市有近20年的马拉松比赛历史,过去全程马拉松名额一直相对较少。而近几年,这一现状大大改变,很多想参加全程马拉松(简称全马)的跑者报不上名。所以该城市近两年也大幅增加“全马”的名额。2017年,参加“全马”的人数比“半马”的人少,但是2018年,2019年参加“全马”的人数呈上升趋势,且每年比前一年均增加25%(即2018年比2017年增加25%,2019年比2018年增加25%),2019年,有12500名“全马”参赛者。
(1)求2017年、2018年“全马”参赛人数;
(2)据赞助食物的某商家反映:2017年与2018年该商家分别给参加“全马”和“半马”的参赛者提供了不同价格的食物,每个“全马”参赛者获得的食物价值高于“半马”参赛者,2017年,商家提供食物共用去22万元;这两年商家是按同一个标准分别给“全马”和“半马”参赛者提供食物(人太多,标准不可轻易提高),即使这样,2018年,虽然参加马拉松比赛的总人数与2017年一样多,但是由于“全马”参赛者人数刚好与“半马”参赛者人数调换了,赞助商比2017年多提供了p万元的食物;商家发现这p万元的食物刚好可以供400名“全马”参赛者和400名“半马”参赛者享用。求p的值。
-
科目: 来源: 题型:
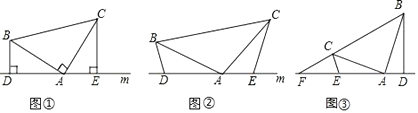
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强课外阅读,开阔视野,我校开展了“书香校园”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制成如下频数分布表和不完整的频数直方
图:


请根据图表信息回答下列问题:
(1)频数分布表中的a=_______,b=_______;
(2)将频数直方图补充完整;
(3)全校共有学生1200人,若规定阅读时间超过2小时则评为“优秀阅读员”,请估计能评为“优秀阅读员”的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M为抛物线
 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.

(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳生活,绿色出行”,自行车成为人们喜爱的交通工具.某品牌共享自行车在温州的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆.
(1)该品牌共享自行车前3个月的投放量的月平均增长率相同,则这三个月一共投放了多少辆自行车?
(2)考虑到增强客户体验,该品牌共享自行车准备投入3万元向自行车生产厂商定制了一批两种规格比较高档的自行车,之后投放到某高端写字楼区域.已知自行车生产厂商生产A型车的成本价为300元/辆,售价为500元/辆,生产B型车的成本价为700元/辆,售价为1000元/辆.根据指定要求,B型车的数量需超过12辆,且A型车的数量不少于B型车的2倍.自行车生产厂商应如何设计生产方案才能获得最大利润?最大利润是多少?
相关试题

