【题目】“低碳生活,绿色出行”,自行车成为人们喜爱的交通工具.某品牌共享自行车在温州的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆.
(1)该品牌共享自行车前3个月的投放量的月平均增长率相同,则这三个月一共投放了多少辆自行车?
(2)考虑到增强客户体验,该品牌共享自行车准备投入3万元向自行车生产厂商定制了一批两种规格比较高档的自行车,之后投放到某高端写字楼区域.已知自行车生产厂商生产A型车的成本价为300元/辆,售价为500元/辆,生产B型车的成本价为700元/辆,售价为1000元/辆.根据指定要求,B型车的数量需超过12辆,且A型车的数量不少于B型车的2倍.自行车生产厂商应如何设计生产方案才能获得最大利润?最大利润是多少?
参考答案:
【答案】(1)这3个月一共投放了2440辆车.(2)生产A型车34辆,B型车13辆,生产商有最大利润为10700元.
【解析】
(1)设前3个月的月平均增长率为x,根据题意列出方程即可求出答案.(2)设生产B型车x辆,根据题意列不等式组,解不等式组得x为13、14、15、根据利润(W)的解析式可知W随x的增大而减小,所以x为13时利润最大,通过解析式求出利润即可.
(1)设前3个月的月平均增长率为x,根据题意得:![]()
解得![]() (舍去)
(舍去)![]()
![]() (辆)
(辆)
答:这3个月一共投放了2440辆车.
(2)①设生产B型车x辆,则生产A型车![]() 辆,根据题意,
辆,根据题意,
得
解得![]() ,
,
∵x为正整数,∴x=13,14,15
设生产产商的利润为W,由题意得
W=(500-300)(60-2x)+(1000-700)x=12000-100x
∵k=-100<0,∴W随x的增大而减小
∴当x=13时,![]() . ∴
. ∴![]() (辆)
(辆)
答:生产A型车34辆,B型车13辆,生产商有最大利润为10700元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙
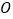 的直径,过点A作⊙
的直径,过点A作⊙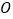 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙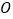 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.(1)求证:
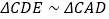 ;
;(2)若AB=2,
 ,求AE的长.
,求AE的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M为抛物线
 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.

(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
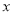 取何值时,下列各式在实数范围内有意义?
取何值时,下列各式在实数范围内有意义?(1)
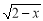 ;
; (2)
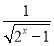 ;
; (3)
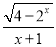 ;
;(4)
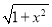 ;
; (5)
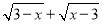 ;
; (6)
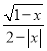 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AB=6cm,AC=8cm,动点P以3cm/s从点B出发向终点C运动;动点Q以1cm/s从点C出发向终点B运动,动点P,Q同时出发,以PQ为直径在BC上方作半圆O,设运动时间为t(s).
(1)当t=1时,半圆O的半径R=_______;
(2)当半圆O落在△ABC的内部(包括边界)时,求t的取值范围;
(3)当点P在Q的左边时,过点P作PE//AB交半圆于点E.,求tan∠EAC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形),△ABC的顶点A,B的坐标分别为:(﹣4,3),(-2,﹣1).
(1)请在图中作出平面直角坐标系并写出点C的坐标;
(2)请作出将△ABC向下平移2个单位长度,再向右平移3个单位长度后的
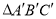 ;并写出点C′的坐标.
;并写出点C′的坐标.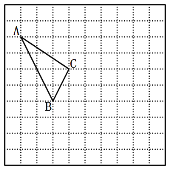
相关试题

